Пошаговое объяснение:
се 4 функции вида y = kx + b. если b > 0, то прямая соприкасается с осью ординат выше оси абсцисс, а если b < 0, то прямая соприкасается с осью ординат ниже оси абсцисс.
Значит, графики A и B соответствуют уравнениям 2 и 3, а графики C и D соответствуют уравнениям 1 и 4. Определим теперь конкретно какой график к какому уравнению подходит.
Рассмотрим уравнение, в котором k = 2
y = 2x + 5, причём x = \frac{5}{2}
2
5
= 2,5. Значит, прямая проходит через точку абсцисс 2,5.
Рассмотрим уравнение, в котором k = 1
y = x - 5, из свойств числового коэффициента b следует, что график проходит через точку ординат -5, а из формулы y = a(x - m)² следует, что точка соприкосновения оси абсцисс и прямой смещена вправо на 5.
Проведя аналогичные рассуждения с остальными двумя уравнениями и их графиками, придём к выводу, что
1) - C
2) - A
3) - B
4) - D
Часть 2.
1. Целые числа: -1, 0, 1, 2. Наибольшее: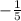
, наименьшее: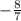 
2. -0.1
3. х = -0.6
4. 96
5. х = -4.9
Часть 3.
1. x₁ = -1.2 х₂ = -2
2. -5
Пошаговое объяснение:
Часть 2.
1.
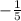= -0.2, наибольшее число из всех, а 
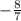= -1 
, следовательно наименьшее из них.
2. Я так понимаю это минус в начале выражения? Если да, то:
-7.35+6.5+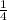
+
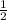= -7.35+6.5+0.25+0.5 = -0.1
3. -1.7+х = -2.3
х = -2.3-(-1.7)
х = -2.3+1.7
х = -0.6
4. -25*(-8)+416:(-4) = 25*8+416:(-4) = 200-104 = 96
5.
х = -4.2
х = -4.2 :
х =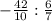
х =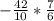
х =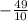
х = -4.9
Часть 3.
1. |x+1.6| = 0.4
|x+
| = 
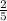
x +
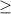0 x + 
< 0
(x+
) - 
= 0 (-х-
) - 
= 0
x +
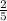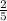= 0 -х-2=0
x₁ =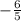
= -1.2 х₂ = -2
2.
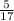* 1.47 - 
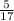* 18.47 = 
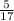* (1.47-18.47) = 
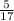* (-17) = -5