1)CB - ребро двугранного угла. Чтобы найти линейный угол двугранного угла, необходимо построить плоскость ⊥ ребру BC. Опустим AE ⊥ BC, DE ⊥ BC по теореме о трех перпендикулярах, где AE - проекция, DE - наклонная. BC - прямая проведенная через основание наклонной и перпендикулярная проекции. AE и DE - находятся в одной плоскости и пересекаются, ВС - перпендикулярна AE и DE ⇒ перпендикулярна плоскости AED ⇒∠AED - линейный угол двугранного угла ∠ABCD. 2) ΔABC - равнобедренный, т.к. AB = AC = 10 см ⇒ опущенный перпендикуляр AE есть медиана ⇒ EC = DC/2 = 6 см. 3) ΔAEC - прямоугольный По т. Пифагора (см) 4) т.к. AD = AE = 8(см) ⇒ ΔADE равнобедренный. ΔADE - прямоугольный и равнобедренный ⇒ ∠AED = 45° ответ: ∠AED = 45°
(см)
На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.
Пошаговое объяснение:
Если его длину увеличить на 15%, а ширину увеличить на 22%, то:
Представим проценты в виде дроби: 0.15 и 0.22, тогда:
Длина a+0.15a = 1.15a; Ширина b+0.22b = 1.22b
S = a*b = 1.15a*1.22b = 1.4ab
Отношение площадей: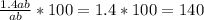
, отнимаем от значения 100% обычной площади и получаем: 140 - 100 = 40%.
На 40% увеличится площадь прямоугольника, если его длину увеличить на 15%, а ширину увеличить на 22%.