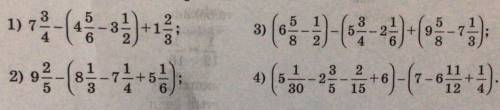
Можно решить, воспользовавшись формулой первых n-чденов геометрической прогрессии.
b₁=2 (бактерии)
q=2 (каждые 8 часов количество бактерий увеличивается вдвое)
S(n)>1000
Найти значение n - деления, за которые количество бактерий сьанет больше 1000.
S(n)=b₁*(1-qⁿ)/(1-q)
2*(1-2ⁿ)/(1-2)>1000
2⁽ⁿ⁺¹⁾>998
Если (n+1)=10, то 2¹⁰=1024
1024>1000>998
n+1=10
n=9 - за 9 делений количество бактерий впервые станет >1000.
В сутки бактерии делятся 3 раза: 24/8=3, значит
9/3=3 - Через трое суток количество бактерий впервые станет
больше 1000
ответ: В. 3
Можно решить простым подсчетом:
1. 2*2=4
2. 4*2=8
3. 8*2=16
4. 16*2=32
5. 32*2=64
6. 64*2=128
7. 28*2=256
8. 256*2=512
9. 512*2=1024
Можно решить, воспользовавшись формулой первых n-чденов геометрической прогрессии.
b₁=2 (бактерии)
q=2 (каждые 8 часов количество бактерий увеличивается вдвое)
S(n)>1000
Найти значение n - деления, за которые количество бактерий сьанет больше 1000.
S(n)=b₁*(1-qⁿ)/(1-q)
2*(1-2ⁿ)/(1-2)>1000
2⁽ⁿ⁺¹⁾>998
Если (n+1)=10, то 2¹⁰=1024
1024>1000>998
n+1=10
n=9 - за 9 делений количество бактерий впервые станет >1000.
В сутки бактерии делятся 3 раза: 24/8=3, значит
9/3=3 - Через трое суток количество бактерий впервые станет
больше 1000
ответ: В. 3
Можно решить простым подсчетом:
1. 2*2=4
2. 4*2=8
3. 8*2=16
4. 16*2=32
5. 32*2=64
6. 64*2=128
7. 28*2=256
8. 256*2=512
9. 512*2=1024
1)67/6
2)63/20
3)29/6
4)119/15
Пошаговое объяснение:
1) 31/3 - (29/6-7/2)+5/3 = 36/3-(29/6-24/6) = 36/3-5/6=72/6-5/6=67/6
2) 47/5-(25/3-29/4+31/6)=47/5-(50/6-29/4+31/6)=47/5-(81/6-29/4)=
=47/5-(27/2-29/4)=47/5-(54/4-29/4)=47/5-25/4 = 188/20-125/20=63/20
3) (53/8-1/2)-(23/4-13/6)+(77/8-22/3)=49/8-43/12+55/24=147/24-86/24+55/24=116/24=29/6
(53/8-1/2)=53/8-4/8=49/8(23/4-13/6)=69/12-26/12=43/12(77/8-22/3)=231/24-176/24=55/244)(150/30-13/5-2/15+6)-(7-83/12+1/4)=124/15-1/3=124/15-5/15=119/15
(150/30-13/5-2/15+6)=5+6-39/15-2/15=11-41/15=165/15-41/15=124/15(7-83/12+1/4)=84/12-83/12+3/12=4/12=1/3