Определённой дроби у нас в условии нет (чисел), так что возьмём универсал - переменные.)
Имеется дробь:
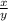
Даже сделаем так:
И в числителе и в знаменателе - числа, которые составляют 100% каждое по отдельности, то есть:
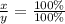
И эти числа, кстати, да - положительные, т.е. оба > 0.
Теперь смотрим условия: числитель увеличивается на 32%, а знаменатель - на 65%. Что это означает? Это означает, что сначала нужно найти сколько составляет 32% от 100% и 65% - от 100%. Есть формула. Хотя она здесь, честно говоря, и не нужна, но всё-таки приведу для справки:
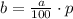
b - это то, что мы получим
a - это число от которого считаем
p - это проценты, которые мы по сути и переводим в конкретное число.
У нас:
b - это то, что мы получим
a - это числа, которые стоят в числителе и знаменателе (для удобства возьмём сотни ("100") за эти числа)
p - это проценты, которые указаны в условии задачи (32% и 65%).
Итак:
b₁ (числитель) = 100 : 100 × 32 = 32
b₂ (знаменатель) = 100 : 100 × 65 = 65
А теперь ещё раз читаем условие задачи: "...если числитель увеличится на 32%, а знаменатель увеличить на 65%". Надо те результаты, которые мы получили, прибавить к числам, от которых находили эти самые результаты:
1. 100 + 32 = 132 (числитель)
2. 100 + 65 = 165 (числитель)
Мы получили изменённую дробь:

Остааётся только разделить полученную дробь на первоначальную, и тогда мы узнаем, на сколько же они различны, вернее ВО сколько:
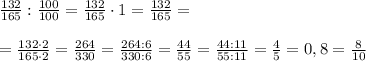
0,8 - это и есть ответ. Дробь изменилась в 0,8 раз или уменьшилась до 80% (или, другими словами: уменьшилась на 20%, так как 100 - 80 = 20). Давайте проверим:
Возьмём, допустим, такую дробь:
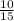
Изменяем числитель и знаменатель согласно условиям:
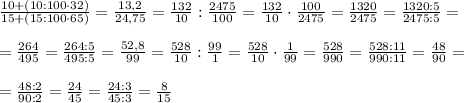
Теперь разделим получившуюся дробь на первоначальную:
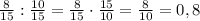
И так с любыми числами, стоящими в числителе и знаменателе.)
ответ: в 0,8 раз или на уменьшится 20%.
ответ: рассмотрим , для решения которых некоторую величину можно принять за одну или несколько частей. при решении таких бывает полезно делать рисунки, облегчающие решение.
1. в двух коробках лежит 120 дисков – в первой коробке в 3 раза больше дисков, чем во второй. сколько дисков лежит в каждой коробке?
решение:
представим содержимое коробок в виде частей. если диски, находящиеся во второй коробке, составляют 1 часть, то в первой коробке – 3 такие части. сделаем схематический рисунок:
на части
1) сколько частей составляют 120 дисков?
1 + 3 = 4 (части)
2) сколько дисков приходится на 1 часть?
120 : 4 = 30 (дисков)
3) сколько дисков находится в первой коробке?
30 · 3 = 90 (дисков)
ответ: 90 – в первой коробке, 30 – во второй.
2. некто заплатил за книжку на 120 рублей больше, чем за тетрадь. известно, что книга дороже тетради в 4 раза. сколько стоит книга?
решение:
представим стоимость в виде частей. если стоимость тетради составляет 1 часть, то стоимость книги составляет 4 такие же части. сделаем схематический рисунок:
решение на части
1) 4 - 1 = 3 (части) – приходится на 120 рублей.
2) 120 : 3 = 40 (рублей) – приходится на 1 часть.
3) 4 · 40 = 160 (рублей) – стоит книга.
ответ: книга стоит 160 рублей.
3. в первой коробке на 6 карандашей больше, чем во второй, а в двух вместе 30 карандашей. сколько карандашей в каждой коробке?
решение:
сделаем схематический рисунок:
на нахождение части
1) если из первой коробки вынуть 6 карандашей, в ней станет столько же карандашей, сколько и во второй:
30 - 6 = 24 (кар.)
2) найдём число карандашей в каждой из коробок:
24 : 2 = 12 (кар.)
3) теперь вернём 6 карандашей в первую коробку:
12 + 6 = 18 (кар.)
ответ: в первой коробке 18 карандашей, во второй – 12.
пошаговое объяснение: