x = 2.6
Пошаговое объяснение:
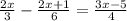
Сначала приведем к общему знаминателю дроби.
Находим наименьшее общее кратное знаменателей дробей. НОК(3, 6, 4) = 12. Это число и будет новым знаменателем.
Чтобы знаменатели всех дробей стали равны 12, числитель и знаменатель первой дроби нужно домножить на 4 = 12:3, числитель и знаменатель второй дроби - на 2 = 12:6,а числитель и знаменатель третей дроби - на 3 = 12:4.

Теперь рассматриваем только числители и решаем уравнение.
8x - (4x+2) = 9x - 15
8x - 4x - 2 = 9x -15
4x - 9x = -15 + 2
-5x = -13

x = 2.6
нод
а) 4 б) 25
нок а) 60 б) 150
Пошаговое объяснение:
б)
Наибольший общий делитель (НОД) двух данных чисел 50 и 75 — это наибольшее число, на которое оба числа 50 и 75 делятся без остатка.
НОД (50; 75) = 25.
Как найти наибольший общий делитель для 50 и 75
Разложим на простые множители 50
50 = 2 • 5 • 5
Разложим на простые множители 75
75 = 3 • 5 • 5
Выберем одинаковые простые множители в обоих числах.
5 , 5
Находим произведение одинаковых простых множителей и записываем ответ
НОД (50; 75) = 5 • 5 = 25
НОК (Наименьшее общее кратное) 50 и 75
Наименьшим общим кратным (НОК) 50 и 75 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (50 и 75).
НОК (50, 75) = 150
Как найти наименьшее общее кратное для 50 и 75
Разложим на простые множители 50
50 = 2 • 5 • 5
Разложим на простые множители 75
75 = 3 • 5 • 5
Выберем в разложении меньшего числа (50) множители, которые не вошли в разложение
2
Добавим эти множители в разложение бóльшего числа
3 , 5 , 5 , 2
Полученное произведение запишем в ответ.
НОК (50, 75) = 3 • 5 • 5 • 2 = 150
а)
Наибольший общий делитель (НОД) двух данных чисел 12 и 20 — это наибольшее число, на которое оба числа 12 и 20 делятся без остатка.
НОД (12; 20) = 4.
Как найти наибольший общий делитель для 12 и 20
Разложим на простые множители 12
12 = 2 • 2 • 3
Разложим на простые множители 20
20 = 2 • 2 • 5
Выберем одинаковые простые множители в обоих числах.
2 , 2
Находим произведение одинаковых простых множителей и записываем ответ
НОД (12; 20) = 2 • 2 = 4
НОК (Наименьшее общее кратное) 12 и 20
Наименьшим общим кратным (НОК) 12 и 20 называется наименьшее натуральное число, которое само делится нацело на каждое из этих чисел (12 и 20).
НОК (12, 20) = 60
Как найти наименьшее общее кратное для 12 и 20
Разложим на простые множители 12
12 = 2 • 2 • 3
Разложим на простые множители 20
20 = 2 • 2 • 5
Выберем в разложении меньшего числа (12) множители, которые не вошли в разложение
3
Добавим эти множители в разложение бóльшего числа
2 , 2 , 5 , 3
Полученное произведение запишем в ответ.
НОК (12, 20) = 2 • 2 • 5 • 3 = 60
45+х=420÷7
сумма +
частное чисел ÷