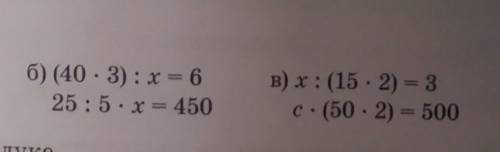
Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки: Ca=A²/C и Cb=B²/C. В нашем случае Cb = 2,25.
Имеем: C=Ca+Cb = 25/C+2,25; Отсюда С²-2,25С-25=0. Решаем это квадратное уравнение.
Детерминант равен √5,0625+100 = √105,0625 = 10,25
Искомая гипотенуза равна (2,25±10,25)/2 = 6,25.
2.катет а=√а1*с, где а1 проекция с гипотенуза
Высота, проведенная из вершины прямого угла, делит гипотенузу на отрезки: Ca=A²/C и Cb=B²/C. В нашем случае Cb = 2,25.
Имеем: C=Ca+Cb = 25/C+2,25; Отсюда С²-2,25С-25=0. Решаем это квадратное уравнение.
Детерминант равен √5,0625+100 = √105,0625 = 10,25
Искомая гипотенуза равна (2,25±10,25)/2 = 6,25.
2.катет а=√а1*с, где а1 проекция с гипотенуза
(40*3):x=6
120:x=6
x=120:6
x=20
25:5*x=450
5*x=450
x=450:5
x=90
x:(15*2)=3
x:30=3
x=30*3=
x=90
c*(50*2)=500
c*100=500
c=500:100
c=5
надеюсь и правильно)