
Пошаговое объяснение:
Построение цветка:
Для наглядности окружности выполнены разными цветами
1. Рассматриваем цветок. Замечаем, что он составлен одинаковыми окружностями. Лепестки голубого цветка в центральной окружности образованы окружностями, центры которых находятся на центральной. Длина лепестка равна радиусу центральной окружности.
2. Строим центральную окружность (красную).
3. Мысленно прокладываем вертикальную линию через центр 1 окружности. Верхняя точка 2 пересечения ее с центральной окружностью будет центром следующей окружности (оранжевой), проводим ее не меняя радиуса (равного радиусу центральной)
4. Эта окружность имеет две точки пересечения с центральной 3 и 7. Тем же радиусом проводим через эти точки две новых окружности (желтую и фиолетовую).
5. Получили новые точки 4 и 6 пересечения вновь построенных окружностей с центральной. Они будут центрами еще двух окружностей (зеленой и синей).
6. Через точку 5 их пересечения ( с центральной) проводим последнюю окружность (голубую)
Раскрашиваем на свой вкус.

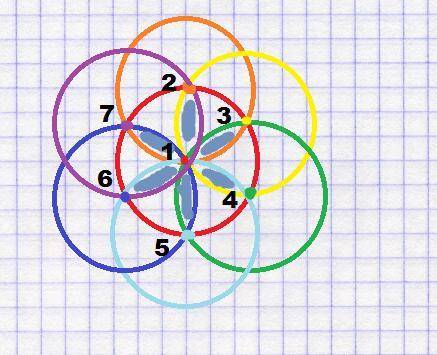

Построение: все окружности одного радиуса.
Первым нарисована центральная окружность (круг). На ней внизу взята в качестве центра произвольная точка, из которой построен второй круг, который пересекает первый в двух точках. Из этих точек нарисованы еще два круга, 3й и 4й; они тоже пересекли 1й круг, и из этих точек построены 5й и 6й круги, а из самой верхней точки 7й круг, последний.
Все. Поскольку радиусы равны, больше новых точек не образуется. Все 6 внешних окружностей при пересечении между собой образовали лепестки
Формулы, которыми мы будем пользоваться:
Длина окружности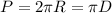
Площадь окружности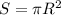
Пошаговое объяснение:
1.1 Утверждение неверное, так как отношение длины окружности к диаметру всегда равно Пи для всех окружностей (см. формулу длины окружности)
1.2 Да, утверждение верное, так как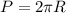 , и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза
, и если мы умножим R на три, то и периметр или длина окружности так же увеличится в три раза
1.3 Данное утверждение неверно, т.к. зависимость площади круга от радиуса не линейна, а квадратична. То есть, если мы уменьшим радиус в два раза, то площадь уменьшится в 4 раза.
1.4 Верно, см. объяснение в 1.3
2. Воспользуемся формулой вычисления длины круга, приведённой вначале:
3. Воспользуемся формулой вычисления площади круга, приведённой вначале: