1) 2arcsin(-1)-4arcctg(-1) = -2π/2-4(π - arcctg1) = -π - 4(π - π/4) = -π - 4(3π/4) = -π - 3π = -4π.
2) ctgx>-1; πn < x < 3π/4 + πn, n∈Z.
3) 5cos^2x-6cosx=0; cosx(5cosx-6)=0;
cosx = 0 або 5cosx-6 = 0.
x = π/2 + πn, n∈Z. cosx = 1,2 - немає розв'язків.
Відповідь: π/2 + πn, n∈Z.
4) tg(arcsin1/2+arccos0) = -√3.
tg(arcsin1/2+arccos0) = tg(π/6+π/2) = -сtg(π/6) = -√3, що й треба було довести.
5) sinx+sin3x/cosx=0. ОДЗ: cosx ≠ 0.
sinx+sin3x = 0; 2sin2xcosx = 0;
sinx = 0 або cosx = 0 - не задовольняє ОДЗ.
x = πn, n∈Z.
6) tg(4x+π/4)+1 ≤ 0; tg(4x+π/4) ≤ -1; -π/2 + πn ≤ 4x+π/4 ≤ -π/4 + πn;
-π/2- π/4 + πn ≤ 4x ≤ -π/4 - π/4 + πn, n∈Z; -3π/4 + πn ≤ 4x ≤ -π/2 + πn, n∈Z;
-3π/8 + πn/4 ≤ x ≤ -π/8 + πn/4, n∈Z.
7) Розв'язати систему рівнянь: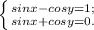 
Додамо перше і друге рівняння системи: 
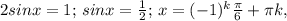k∈Z.
Віднімемо друге і перше рівняння системи:
±
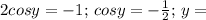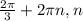∈Z.
Відповідь: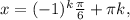 
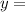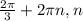k∈Z; 
±∈Z.
2-х-√х+10=0
2-х=√х+10
(2-х)²=(√х+10)²
4-2х+х²=х+10
х²-3х-6=0
Д=в²-4ас=9-4·1·(-6)=9+24=33
Х1=3-√33/2 , Х2= 3+√33/2
Проверка:
Х1=3-√33/2,-явл.т.к (3-√33/2)²-3(3-√33)/2-6=0,(9-6√33+33)/4 -3·2(3-√33)/4-6=
=(9-6√33+33-18+6√33)/4-6=24/4-6=6-6=0,0=0
Х2=3+√33/2-явл. т.к. (3+√33/2)²-3(3+√33)/2-6=(9+6√33+33-18-6√33)/4-6=24/4-6
=6-6=0,0=0
ответ: 3-√33/2;3+√33/2
2)
х²-х+√х²-х-2=8
Пусть :х²-х=у
у+√у-2=8
у-8=√у-2
(у-8)²=(√у-2)²
у²-16у+64=у-2
у²-17у+66=0
У1+У2=17
У1·У2=66
У1=11,У2=6
х²-х=У1
х²-х=11
х²-х-11=0
Х1=(1-3√5)/2, Х2=(1+3√5)/2
Проверка:
Х1=(1-3√5)/2, -не явл. корнем т.к. при подстановки в данное уравнение, получим:14≠8
Х2=(1+3√5)/2-не явл корнем, т.к. 14≠8
У2= 6
х²-х=6
х²-х-6=0
Х3=-2
Х4=3
Проверка:
х=3- явл. корнем,т.к 3²-3+√3²-3-2=6+√4=6+2=8, 8=8
х=-2-явл. корнем,т.к (-2)²+2+√(-2)²+2-2=6+√4=6+2=8, 8=8
ответ: -2;3.