Найдем максимальное количество одинаковых чисел.
Рассмотрим любое число на доске. Для данной суммы числа с его последними тремя цифрами существует не более одной подобной суммы, но уже с другим числом. Иначе говоря, ![1000a+100b+10c+d+[100b+10c+d]=1000m+100n+10k+l+[100n+10k+l], \;\; 0\leq b,c,d,n,k,l\leq 9, \;\;0](/tpl/images/0922/2237/a86dd.png)
- имеет единственное решение для данных чисел a,b,c,d; Пусть это выполняется для чисел на доске. Теперь рассмотрим числа в тетради. Из вышесказанного следует, что эти 88 чисел можно разбить определенным образом на 44 пары, где в каждой паре будет два одинаковых числа. То есть может получиться 44 одинаковых числа. Но это с одной стороны. Рассмотрим другую сторону. Заметим, что сумма всех чисел нечетна - 999 999. Следовательно, в этой сумме есть хотя бы одно нечетное число. Взглянем на сумму числа с его тремя последними цифрами: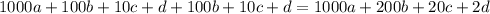 
; Если число четное, то d - четно, значит результат делится на 4. Если d - нечетно, то результат не делится на 4. Раз существует хотя бы одно нечетное число, то рассмотрим одну из 44-ех пар, где четное и нечетное число. В самом начале мы сказали, что в 44 парах равные числа. Но из вышесказанного следует противоречие - сумма четного числа с его последними тремя цифрами не может равняться сумме некоего нечетного числа с его последними тремя цифрами, поскольку последнее не делится на 4, в отличие от четного. Это означает, что хотя бы одна пара будет содержать разные числа. То есть максимальное количество одинаковых чисел равно 44-1=43. А минимальное количество различных чисел равно 88-43 = 45. Значит всегда найдется по крайней мере 45 различных чисел.
2sin²x + sinx*cosx = 1,
sinx*cosx = 1 - 2sin²x,
Т. к. sinx*cosx ≡ (1/2)*(2*sinx*cosx) ≡ (1/2)*sin(2x),
1 - 2sin²x ≡ cos²x - sin²x ≡ cos(2x), то
имеем
(1/2)*sin(2x) = cos(2x), (*)
если cos(2x) = 0, тогда получаем (1/2)*sin(2x) = 0, и sin(2x) = 0, но это противоречит основному тригонометрическому тождеству:
cos²(2x) + sin²(2x) ≡ 1.
Поэтому cos(2x) ≠ 0, и домножим равенство (*) на 2/(cos(2x)),
получим
(1/2)*sin(2x)*2/cos(2x) = cos(2x)*2/cos(2x),
sin(2x)/cos(2x) = 2,
Т.к. sin(2x)/cos(2x)≡ tg(2x), то получаем
tg(2x) = 2.
15*(e+2)/7=6*(2e+7)/7
15*(е+2)=6* (2e+7)
15е+30=12е+42
15е-12е=42-30
3е=12
е=4
5*(c+3)/6=8*(10-c)/6
5*(c+3)= 8*(10-c)
5с+15=80-8с
5с+8с=80-15
13с=65
с=5