Это простейшие производные.
Рассмотрим общий случай:
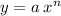
а – просто коэффициент при Х, n – степень Х.
Производная функции у, обозначаемая обычно у' или dy/dx, будет иметь следующий вид:
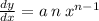
Ничего сложного.
Рассмотрим несколько частных случаев из Ваших примеров.
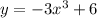
Здесь коэффициент а равен (–3), степень n равна 3. Значит, по правилу, представленному выше, производная будет иметь вид:
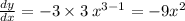
При числе 6 нет «Х», поэтому при взятии производной это число просто пропадает.
Другой частный пример:
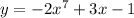
Берём производную от каждой части по отдельности.
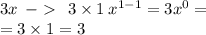
Итого:
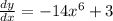
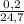≈ 0.008
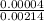≈0.018 ≈1.8%
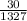≈ 0.02≈2%
ответ:Решение:
5x³-5x=0
5x(x²-1)=0
5x(x-1)(x+1)=0
x(x-1)(x+1)=0
x₁=0
x₂=1
x₃=-1
2)
64x³-16x²+x=0
x(64x²-16x+1)=0
x(8x-1)²=0
x₁=0
8x-1=0
8x=1
x=
3)
x³-3x²-4x+12=0
x²(x-3)-4(x-3)=0
(x²-4)(x-3)=0
(x-2)(x+2)(x-3)=0
x₁=2
x₂=-2
x₃=3
Пошаговое объяснение: