Имеем многочлен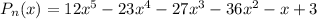 
Корнями многочлена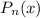 
называют корни уравнения
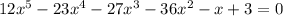
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: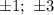 
Подставим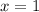 
в корень уравнения и получим:
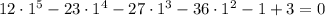
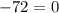— неправда
Подставим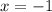 
в корень уравнения и получим:
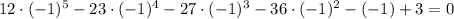
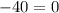— неправда
Подставим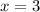 
в корень уравнения и получим:
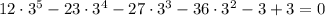
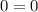— правда
Следовательно,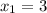 
— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на 
(см. вложение).
После этого исходное уравнение можно записать разложив на множители:
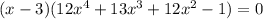
Решаем второе уравнение:
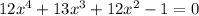
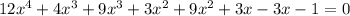
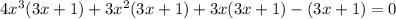
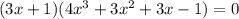
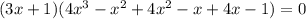
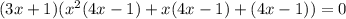
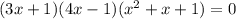
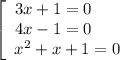
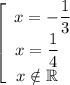
Рациональные корни: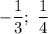 
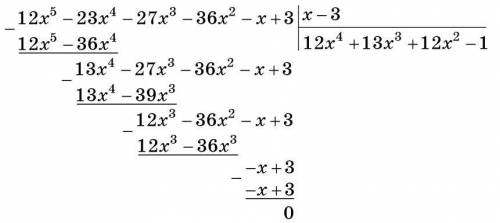
Имеем многочлен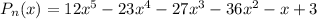
Корнями многочлена 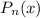называют корни уравнения
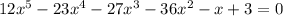
Имеем уравнение пятого порядка. Попробуем его решить с теоремы Безу.
Суть этой теоремы в том, что если уравнение вида с ненулевым свободным членом имеет некий корень , принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Выпишем все делители свободного члена: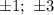
Подставим 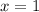в корень уравнения и получим:
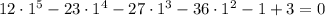
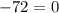— неправда
Подставим 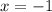в корень уравнения и получим:
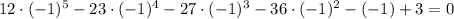
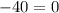— неправда
Подставим 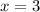в корень уравнения и получим:
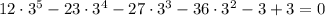
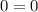— правда
Следовательно, 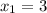— один из корней уравнения. Теперь необходимо выполнить деление многочлена столбиком на (см. вложение).
После этого исходное уравнение можно записать разложив на множители:
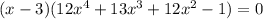
Решаем второе уравнение:
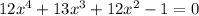
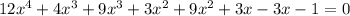
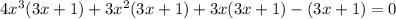
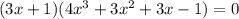
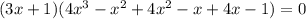
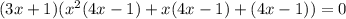
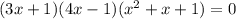
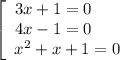
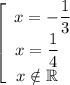
Рациональные корни: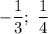
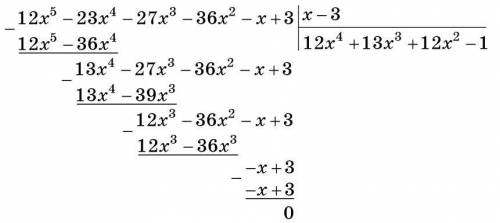
Відповідь:
Покрокове пояснення:
Спочатку вартість збільшилась на 20 відсотків(було 100％,стало 120％)
140*1.2=168 грн
Потім знизили(100-25=75)
168*0.75=126 грн
Відповідь 126 грн
140 - 100％
126 - x
x=126*100/140=90％
100-90=10
Ціна впала на 10％.