Пошаговое объяснение:
9x²+5y²+18x–30y+9=0
1. Определение типа кривой.
квадратичная форма
B = 9x² + 5y²
приводим к каноническому виду
матрица этой квадратичной формы:
9 0
0 5
собственные числа и собственные векторы этой матрицы
(9 - λ)*х₁+ 0y₁ = 0
0x₁ + (5 - λ)y₁ = 0
характеристическое уравнение
λ² - 14λ + 45 = 0 ⇒ λ₁ = 9; λ₂=5
λ₁ > 0; λ₂ > 0 - это эллипс
теперь надо выделить полные квадраты
для х
9(x²+2x + 1) -9= 9(x+1)²-9
и для у
5(y²-2*3y + 3²) -5*3² = 5(y-3)²-45
и получим
9(x+1)²+5(y-3)² = 45
делим на 45 и получаем каноническое уравнение эллипса
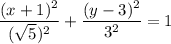
2) координаты фокусов, вершин и центра
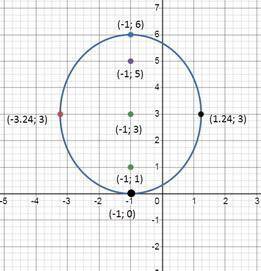
центр C(-1; 3)
полуоси
меньшая a = √5;
большая b= 9
координаты фокусов
F₁(-c;0) и F₂(c;0), где c - половина расстояния между фокусами
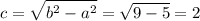
координаты фокусов F₁(-2;0) и F₂(2;0)
с учетом центра, координаты фокусов равны: F₁(-1;1) и F₂(-1;5)
вершины
х = -1; (у-3)²=9 ⇒ у₁ = 0, у₂ = 6
тогда вершины по оси оу (-1; 0) (-1; 6)
у= 3; (х+1)²=5 ⇒ х₁ = -1+√5 ≈1,24; х₂ = -1-√5 ≈ -3,24
и тогда вершины по оси ох (-1+√5; 3) (-1-√5; 3)
P(великий квадрат) = 12 (см), P(малий квадрат) = 4 (см).
Пошаговое объяснение:
1) Периметр квадрата обчислюється за формулою
P = 4 * a, де P - периметр, а - сторона квадрата.
2) Обчислимо периметр великого квадрата, що має сторону 3 см:
P(великий квадрат) = 4 * 3 = 12 (см)
3) Якщо розбити квадрат на 9 різних квадратів, це означає, що площа стала у 9 разів менше, тобто
S(малий квадрат) = 1/9 * S(великий квадрат)
4) Площа квадрата обчислюється за формулою
S = а², де S - площа, а - сторона квадрата
5) Знайдемо площу великого квадрата, що має сторону 3 см:
S = 3² = 9 (см²)
6) Із пункту 3 маємо, що площа малого квадрату дорівнює
S(малий квадрат) = 1/9 * 9 = 1 (см²)
7) Оскільки у квадрата всі сторони рівні, і площа квадрата дорівнює добутку його сторін, отримуємо, що сторона малого квадрата дорівнює 1 см.
8) За формулою із першого пункту обчислимо периметр малого квадрата зі стороною 1 см:
P(малий квадрат) = 4 * 1 = 4 (см).
Це з ВІДОМИХ простих чисел. А так Евклід довів, що не існує найбільшого простого числа
(23021337 - 1) = 23021336
Сума цифр числа 23021337 ділиться на 3, отже це число ділиться на 3, значить 23021337 непроста число.
Остання цифра числа 23021336 позначає парне число, значить 23021336 ділиться на 2, отже 23021336 не проста.
Відповідь: помилка 23021337 і (23021337 - 1) = 23021336 не прості числа.