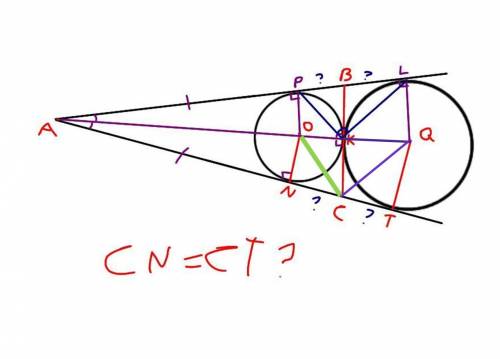
1) Рассмотрим ΔONC и ΔOKC.
У них:
∠ONC= ∠OKC=90°
ON=OK=r (радиусы одной окружности)
сторона OC-общая
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого треугольника, то такие треугольники равны.
Из равенства треугольников следует равенство соответственных сторон.
ΔONC = ΔOKC => CN=KC
2) Рассмотрим ΔQKC и ΔQTC (рассуждаем аналогично)
У них
∠QKC= ∠QTC=90°
ON=OK=R (радиусы одной окружности)
QC-общая
ΔQKC = ΔQTC => КС=CT
3) Если CN=KC, а KC = CT, то => CN=CT Если каждая из двух данных сторон равна третьей, то эти стороны равны между собой (свойство транзитивности).
Доказано.
6+6+2=14
Пошаговое объяснение:
6 с львиный головами
6 с крыльями
2 и то и то