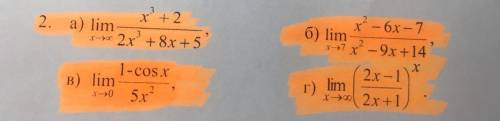
точка (1;1)
Пошаговое объяснение:
Точки экстремума - точки, в которых производная функции равна 0.
y'(x) = ((4x)'*(x+1)² - ((x+1)²)'(4x)) / (x+1)^4 = 0
(по формуле (u/v)' = (u'v - v'u)/(v²) )
4*(x+1)² - 2(x+1)*4x = 0 (дробь равна 0 когда числитель равен 0)
4x² + 8x + 4 - 8x² - 8x = 0
-4x² + 4 = 0
x = ±1
Заметим, что -4x²+4 отрицательна при x<-1 и x>1, и положительна при x∈(-1;1). Значит, и y'(x) отрицательна при x<-1 и x>1, и положительна при x∈(-1;1) (так как (x+1)^4 > 0). При этом, при x = 1, y'(x) = 0, а при x = -1 значение y(x) не определено. Поэтому есть только 1 точка экстремума (максимума): x = 1. Тогда y = 1.
итальянский математик-самоучка, инженер фортификационных сооружений.Родился в городе Брешиа. Настоящая фамилия — Фонтана.Отца своего, конного почтальона, он звал по имени Микелетто В 1506 году отец умер.В оставленных Тартальей сочинениях он рассматривает не только вопросы математики, но и некоторые вопросы практической механики, и топографии.По словам Тартальи, он самостоятельно открыл общий алгоритм решения кубических уравнений, несколько ранее найденный Сципионом дель Ферро. В 1539 году Тарталья передал описание этого метода Дж. Кардано, который поклялся не публиковать его без разрешения Тартальи. Несмотря на обещание, в 1545 году Кардано опубликовал этот алгоритм в работе «Великое искусство», и по этой причине он вошёл в историю математики как «формула Кардано».
Пошаговое объяснение:
а)
б)
так как числитель и знаменатель обращаются в нуль при x=7, то 7 – корень обоих многочленов, а значит, каждый из них разлагается на множители, одним из которых будет (x - 7) .
x² -6x -7 = (x-7)(x+1)
x² - 9x +14 = (x-7)(x-2)
и тогда получим
в)
1-cos = 2sin²(x/2)
следствию свойства первого замечательного предела
sinx ≈ x, тогда 2sin²(x/2) ≈x²/2
и вот что получилось
г)
здесь применим свойство второго замечательного предела