Значит остаток будет 2.
Пошаговое объяснение:
b)2 этот ответ правильный

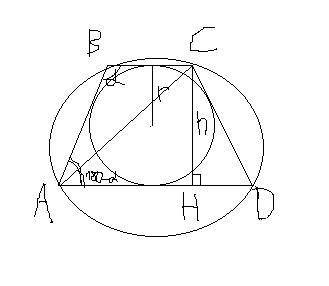
1. Чтобы найти радиус описанной около трапеции окружности, заметим, что эта окружность описана ещё и около треугольника ABC, из теоремы синусов 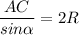
Надо найти AC.
Это можно сделать через теорему косинусов в треугольнике ABC.
Но для этого надо знать AB=a (боковая сторона трапеции) и BC=b (меньшее основание)
Нам же известен угол и радиус вписанной окружности.
Известный факт, что в трапецию если можно вписать окружность, то сумма противоположных сторон равна. 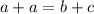 (c- большее основание).
(c- большее основание).
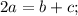
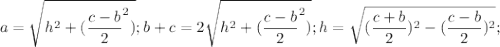

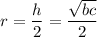
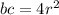
Далее из треугольника CHD ∠CDH=180-α;
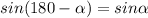
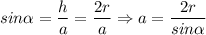
Далее имеем систему с неизвестными b и c:
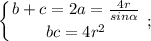
Из 2-го уравнения имеем 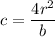
Подставляем в 1-е и получаем:
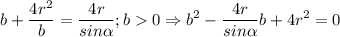
Это квадратное уравнение относительно b:
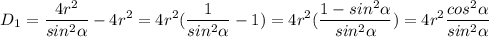
Все величины положительны, поэтому модули 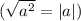 раскрываются с "+".
раскрываются с "+".
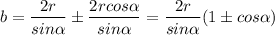
Не понятно пока, оставлять ли оба значения или брать одно, Попробуем вычислить с:
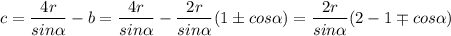
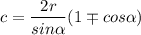
Надо учесть, что b<c. Всё будет зависеть от знаков, которые мы берем.
Чтобы с было больше b,  с "+",
с "+", 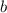 с "-".
с "-".
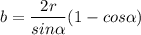
Но нам  толком и не надо. Только
толком и не надо. Только 
Теперь запишем теорему косинусов (AC=d):
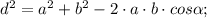
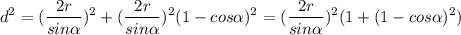
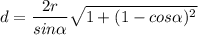
Вспоминаем 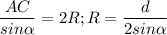
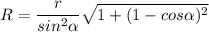
Дальше я не вижу смысла преобразовывать тригонометрию, там вроде ничего путного не выходит.
ответ: 
c)1