56
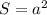 .
.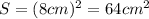 , а площадь каждого маленького квадрата
, а площадь каждого маленького квадрата  .
.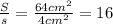 . Итак, у Гриши из одного большого квадрата получилось 16 маленьких. Это ответ на первый вопрос.
. Итак, у Гриши из одного большого квадрата получилось 16 маленьких. Это ответ на первый вопрос. , всего же в ряду, выложенном Гришей, 16 квадратов. Тогда длина ряда будет:
, всего же в ряду, выложенном Гришей, 16 квадратов. Тогда длина ряда будет:  . Это ответ на второй вопрос.
. Это ответ на второй вопрос.
1) 17
2) 49
вот правильные ответы