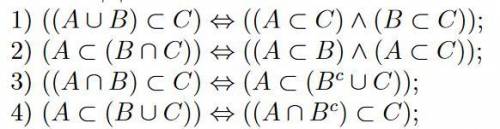
В квадрате из 10 плиток должно быть 100 плиток. Следовательно, количество плиток меньше 100.
Разница 6 плиток возникает после 6 ряда.
Объяснение:
Ряды по "9". Ряды по "8"
9 плиток - полный ряд по "9" 1 ряд по "8" +1 во втором ряду.
18 плиток - 2 полных ряда по "9" 2 ряд по "8" +2 в третьем ряду.
и так далее ... .
В неполном ряду по "8" должно быть 7 плиток.
В неполном ряду по "9" должна быть 1 плитка. Тогда выполняется условие 7-1=6 плиток.
Это происходит в 7 ряду:
8*6=48+7= 55 плиток ˂100
9*6=54+1= 55 плиток ˂100
ответ: осталось 55 плиток.
Объяснение:
Ряды "8". Ряды "7"
8 плиток - полный ряд "8" 1 ряд "7"+1 во втором ряду.
16 плиток 2 полных ряда "8" 2 ряда "7" +2 в третьем ряду
и так далее ... .
В неполном ряду "7" должно быть + 6 плиток. В неполном ряду "8" +1 плитка. Тогда выполняется условие 6-1=5
7*5=35+6= 41 плитка
8*5=40+1= 41 плитка
Всё логично и понятно.
Есть второй ответ - 97 плиток.
Решается через неравенство 7а+6<100; a <13,4; отсюда, а=13, 13*7+6=97, проверка: 12*8+1=97
Все условия задачи, в том числе ограничение в 100 плиток выполнены.
Я докажу первое и последнее, остальное - сам.
1)
Доказательство "⇒".
Пусть у нас дано ((A∪B)⊂C), докажем тогда, что
1.1) A⊂C,
и
1.2) B⊂C.
1.1) x∈A⊂A∪B, ⇒ x∈A∪B⊂С, ⇒ x∈C. То есть A⊂C.
1.2) x∈B⊂A∪B, ⇒ x∈A∪B⊂C, ⇒ x∈C. То есть B⊂C.
чтд.
Доказательство "<=".
Пусть у нас дано: A⊂C и B⊂C. Докажем тогда, что
A∪B⊂C.
Пусть x∈A∪B, ⇔ x∈A или x∈B.
a) x∈A⊂C, ⇒ x∈C.
б) x∈B⊂C, ⇒ x∈C.
То есть A∪B⊂C.
чтд.
4)
Доказательство "⇒".
Пусть у нас дано (A⊂(B∪C)). Докажем тогда, что
Пусть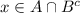 , ⇔
, ⇔ 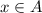 и
и 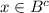 , ⇔
, ⇔
Тогда т.к. A⊂B∪C, имеем
Первый случай. Если x∈B и x∉B, то x∈∅⊂C ⇒ x∈C.
Второй случай. Если x∈C и x∉B, то x∈C\B⊂C, ⇒ x∈C.
чтд.
Доказательство "<=".
Пусть у нас дано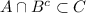 , докажем тогда, что
, докажем тогда, что
A⊂ B∪C.
Пусть x∈A. Тут возможны два варианта x∈B, либо x∉B.
Случай первый: x∈A и x∈B, ⇒ x∈A∩B⊂B, ⇒ x∈B⊂B∪C, ⇒ x∈B∪C.
Случай второй: x∈A и x∉B, ⇒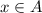 и
и 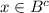 , ⇒
, ⇒
⇒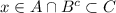 , ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
, ⇒ x∈C⊂B∪C, ⇒ x∈B∪C.
чтд.