Угол между прямой AA1 и плоскостью ABC1 равен
arcsin(√6/3). Угол ≈ 54,7°
Пошаговое объяснение:
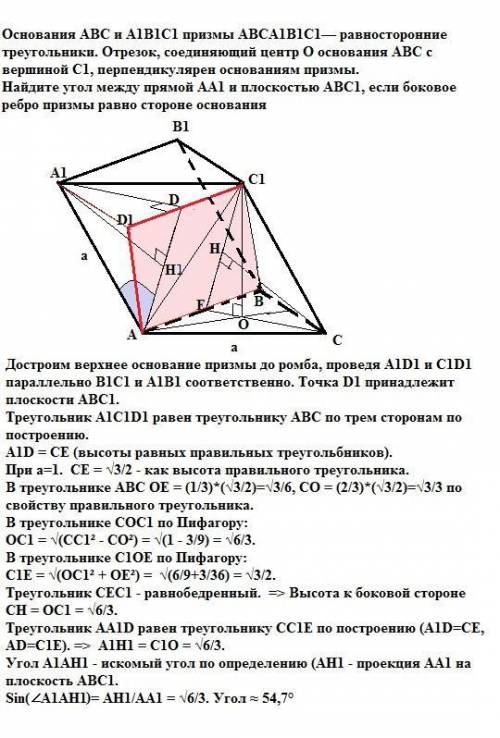
Достроим верхнее основание призмы до ромба, проведя A1D1 и C1D1 параллельно B1C1 и A1B1 соответственно. Точка D1 принадлежит плоскости АВС1.
Треугольник А1С1D1 равен треугольнику АВС по трем сторонам по построению.
A1D = CE (высоты равных правильных треугольбников).
При а=1. CE = √3/2 - как высота правильного треугольника.
В треугольнике АВС ОЕ = (1/3)*(√3/2)=√3/6, СО = (2/3)*(√3/2)=√3/3 по свойству правильного треугольника.
В треугольнике СОС1 по Пифагору:
ОС1 = √(СС1² - СО²) = √(1 - 3/9) = √6/3.
В треугольнике С1ОЕ по Пифагору:
С1Е = √(ОС1² + ОЕ²) = √(6/9+3/36) = √3/2.
Треугольник CEC1 - равнобедренный. => Высота к боковой стороне СН = ОС1 = √6/3.
Треугольник АА1D равен треугольнику СС1Е по построению (A1D=CE, AD=C1E). => A1H1 = C1O = √6/3.
Угол A1АН1 - искомый угол по определению (AH1 - проекция АА1 на плоскость АВС1.
Sin(∠A1AH1 = AH1/AA1 = √6/3. Угол ≈ 54,7°
1 т=10 ц ⇒ 450 т=4 500 ц
1) 4 500:15=300 (ц) или 30 (т) - огурцов собрали с одной (каждой) теплицы в году.
2) 300+5=305 (ц) или 30т 5ц - огурцов собрали с одной (каждой) теплицы в этом году.
3) 305·15=4 575 (ц) или 457т 5ц - огурцов собрали с 15 теплиц в этом году.
ответ: 457т 5ц огурцов собрали с 15 теплиц за этот год.
1) 450:15=30 (т) - огурцов собрали с одной (каждой) теплицы за год.
1 т=10 ц ⇒ 30 т=300 ц
2) 300+5=305 (ц) или 30т 5ц - огурцов собрали с одной (каждой) теплицы за этот год.
3) 305·15=4 575 (ц) или 457т 5ц - огурцов собрали с 15 теплиц в этом году.
ответ: 457т 5ц огурцов собрали с 15 теплиц за этот год.
Мозете мне кто то с алгеброй