Пошаговое объяснение:
№1Воспользуемся свойствами логарифма
x∈(-1/3, +∞)
log3 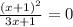
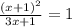
Умножаем обе части на знаменатель и перемещаем все влево:
x^2+2x+1-3x-1=0
x^2-x=0
отсюда
x=0 x=1
№2Алгоритм такой же как в первом(одз, двойку переносим в степень, затем в один логарифм, приравниваем к единице, решаем уравнение)
ответ x=4
№3x∈(1/3, +∞)
log₂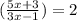
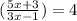
решаем уравнение
5x+3=12x-4
-7x=-7
x=1
№4одз:
x<3/2
умножаем обе части на 1/2 и убираем логарифм
решаем уравнение
3-2x<1
-x<-1
x>1
x∈(1;3/2)
№5x>2/3
3x-2<1
x=1
x∈(2/3;1)
№6умножаем обе части на то нечто в начале
одз
x<1/2
3-2x>=1
x<=1
x∈(-∞;1]
№7одз
x>1/2
умножаем обе части на 1/3 и убираем логарифм
2x-1>=1
x=1
x∈[1;+∞)
№8одз
x∈R
убираем логарифм
x^2-5x+7=3
x^2-5x+4
x=4 x=1
№9одз
x>0
заменяем логарифм на t
t^2+t-2=0
t1=-2
t2=1
log3(x)=-2
log3(x)=1
x=1/9
x=3
Наибольший общий делитель НОД (72; 120) = 24
Наименьшее общее кратное НОК (72; 120) = 360
Пошаговое объяснение:
Наибольший общий делитель::
Разложим числа на простые множители и подчеркнем общие множители чисел:
72 = 2 · 2 · 2 · 3 · 3
120 = 2 · 2 · 2 · 3 · 5
Общие множители чисел: 2; 2; 2; 3
НОД (72; 120) = 2 · 2 · 2 · 3 = 24
Наименьшее общее кратное:
Разложим числа на простые множители. Сначала запишем разложение на множители самого большого число, затем меньшее число. Подчеркнем в разложении меньшего числа множители, которые не вошли в разложение наибольшего числа.
120 = 2 · 2 · 2 · 3 · 5
72 = 2 · 2 · 2 · 3 · 3
НОК (72; 120) = 2 · 2 · 2 · 3 · 5 · 3 = 360
Наибольший общий делитель НОД (72; 120) = 24
Наименьшее общее кратное НОК (72; 120) = 360
Пошаговое объяснение:
Сейчас все решу подожди