Пошаговое объяснение:
По условию задачи площадь S поля разбита на 3 части (по дням).
В первый день тракторная бригада вспахала 30% всего поля, то есть 30% * S = 0,3 * S га.
Во второй день бригада вспахала 75% остального. Поскольку, осталось (1 - 0,3) * S га = 0,7 * S га, то тракторной бригадой вспахано 0,75 * 0,7 * S га = 0,525 * S га.
В третий день вспахано оставшихся 14 га.
Имеем 0,3 * S га + 0,525 * S га + 14 га = S га или (1 - 0,3 - 0,525) * S = 0,175 * S = 14 га, откуда S = (14 : 0,175) га = 80 га.
ответ: (2, -1, 1)
Пошаговое объяснение: Запишем систему уравнений в матричном виде.
![\left[\begin{array}{cccc}3&-1&2&9\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/e1322.png)
Приведем к ступенчатому виду. Применяем операцию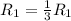 
к 
(к 1 строке) для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\2&3&-1&0\\2&4&3&3\end{array}\right]](/tpl/images/1055/0577/6eddc.png)
Применяем операцию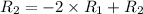 
к 
(ко 2 строке) для того, чтобы сделать некоторые элементы строки равными 0.
Применяем операцию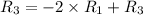 
к 
(к 3 строке) для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&\frac{11}{3} &-\frac{7}{3}&-6 \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/0d2b8.png)
Применяем операцию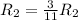 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&-\frac{1}{3} &\frac{2}{3} &3\\0&1&-\frac{7}{11} &-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/8a8f7.png)
Применяем операцию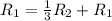 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&\frac{14}{3} &\frac{5}{3} &-3\end{array}\right]](/tpl/images/1055/0577/c212b.png)
Применяем операцию 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&\frac{51}{11} &\frac{51}{11} \end{array}\right]](/tpl/images/1055/0577/960ac.png)
Применяем операцию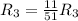 
к для того, чтобы сделать некоторые элементы строки равными 1.
![\left[\begin{array}{cccc}1&0&\frac{5}{11}&\frac{27}{11} \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/ffa18.png)
Применяем операцию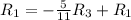 
к для того, чтобы сделать некоторые элементы строки равными 0.
![\left[\begin{array}{cccc}1&0&0&2 \\0&1&-\frac{7}{11}&-\frac{18}{11} \\0&0&1 &1 \end{array}\right]](/tpl/images/1055/0577/a5101.png)
Применяем операцию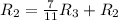 
к для того, чтобы сделать некоторые элементы равными 0.
![\left[\begin{array}{cccc}1&0&0&2\\0&1&0&-1\\0&0&1&1\end{array}\right]](/tpl/images/1055/0577/927aa.png)
Воспользуемся полученной матрицей для того, чтобы описать итоговое решение системы уравнений.
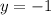
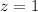
Решением является множество упорядоченных пар, которые удовлетворяют системе.
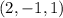
Пошаговое объяснение:
5,70 5,700 взаимно обратные числа