1. 8Х + 10 = 3Х - 10
8Х - 3Х = - 10 - 10
5Х = - 20
Х = - 20 : 5
Х = - 4
ответ: Х = - 4
2. 10 * (У - 2) - 12 = 14 * (У - 2)
10У - 20 - 12 = 14У - 28
10У - 14У = 20 + 12 - 28
- 4У = 4
У = 4 : (- 4)
У = - 1
ответ: У = - 1
3. - 25 * (- 8Х + 6) = - 750
200Х - 150 = - 750
200Х = - 750 + 150
200Х = - 600
Х = - 600 : 200
Х = - 3
ответ: Х = - 3
4. - 10 * (- 4Х + 10) = - 300
40Х - 100 = - 300
40Х = - 300 + 100
40Х = - 200
Х = - 200 : 40
X = - 5
ответ: Х = - 5
5. 3 * (5У - 6) = 16У - 8
15У - 18 = 16У - 8
15У - 16У = - 8 + 18
- У = 10
У = - 10
ответ: У = - 10
6. - 5 * (3Х + 1) - 11 = - 1
- 15Х - 5 - 11 = - 1
- 15Х = - 1 + 5 + 11
- 15Х = 15
X = 15 : ( - 15)
Х = - 1
ответ: Х = - 1
7. - 8У + 4 = - 2 * (5У + 6)
- 8У + 4 = - 10У - 12
- 8У + 10У = - 12 - 4
2У = - 16
У = - 16 : 2
У = - 8
ответ: У = - 8
8. 20 + 30Х = 20 + Х
30Х - Х = 20 - 20
29Х = 0
X = 0 : 29
Х = 0
ответ: Х = 0
9. 26 - 5У = 2 = 9у
14У = 24
У = 24 : 14
У =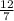 
≈ 1.71428571428571
ответ: У = 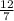≈ 1.71428571428571
Вот Так!
ответ: 1) dz=e^(x/y)*dx/y-x*e^(x/y)*dy/y²; 2) функция имеет максимум в точке M(2/3; 1/3).
Пошаговое объяснение:
1) z=e^(x/y)
Находим частные производные:
dz/dx=1/y*e^(x/y), dz/dy=-x/y²*e^(x/y).
Полный дифференциал dz=dz/dx*dx+dz/dy*dy=e^(x/y)*dx/y-x*e^(x/y)*dy/y²
2) Находим первые частные производные:
dz/dx=2*y+2*x-2; dz/dy=2*x+8*y-4.
Приравнивая их к нулю, получаем систему уравнений:
x+y-1=0
x+4*y-2=0
Решая её, находим x=2/3, y=1/3 - координаты единственной критической точки М(2/3; 1/3).
Находим вторые частные производные:
d²z/dx²=2; d²z/dxdy=2; d²z/dy²=8. Так как они суть постоянные числа, то и в критической точке они будут иметь те же значения:
A=d²z/dx²(M)=2; B=d²z/dxdy(M)=2; C=d²z/dy²(M)=8.
Так как выражение A*C-B²=2*8-4=12>0, то есть положительно, то в точке М функция действительно имеет экстремум. А так как при этом A=2>0, то этот экстремум является максимумом.
Пошаговое объяснение:
Область определения D(f) =R (все действительные числа)
Область значений: E(f) = [-1; +∞)
Убывание на промежутке х∈ (-∞; 2]
Возрастание на промежутке х∈ [2; +∞)
Функция положительна при х∈ (-∞; 1)∪(3; +∞)
Функция отрицательна при х∈ (1; 3)
Нули функции: х₁=1; х₂=3
Функция не является ни четной, ни нечетной.
Функция не является периодической.
Функция имеет единственный экстремум минимум функции: у= -1 в точке х=2
Наименьшее значение функции: у = -1
Функция у = х² - 4х + 3 является степенной квадратичной функцией с графиком типа парабола.
X=-4
2)10y-20-12=14y-28
4y=-4
Y=-1
3)200x-150=-750
200x=-500
X=-2,5
4)40x-100=-300
40x=-200
X=-5
5)15y-18=16y-8
Y=-10
7)-15x-5-11=-1
-15x=15
X=-1
8)-8y+4=-10y-12
2y=-16
Y=-8
9)29x=0
X=0
10)14y=24
Y=24/14
Y=12/7