
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
ответ: – 8.
Пример 3. Решите уравнение .
. Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
ответ: 3.
Пример 4. Решите систему
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
ответ: (1; 1).
Замечание. Если неизвестные системы х и у, то ответ можно записать в виде ко
Пошаговое объяснение:
надеюсь правильно
400
Пошаговое объяснение:
Требуется вычислить сумму
S = 1 + 3 + 5 + ... + 35 + 37 + 39
Количество слагаемых равно (39-1):2+1=38:2+1=19+1=20.
Первый член арифметической прогрессии a₁=1, разность d=2. Нужно вычислить сумму первых n=20 членов прогрессии. Так как последний член прогрессии a₂₀=39, то можно использовать формулу
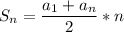 .
.
Тогда
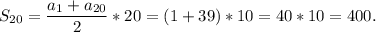
Перепишем сумму в двух видах
S = 1 + 3 + 5 + ... + 35 + 37 + 39
S = 39 + 37 + 35 + ... + 5 + 3 + 1
Так как количество слагаемых 20, то сумма обоих сумм равна
2·S = (1+39)+(3+37)+(5+35)+ ... +(5+35)+(3+37)+(1+39) =
=40+40+40+...+40+40+40=40·20
или
S = 40·20:2= 800:2=400.
В решении.
Пошаговое объяснение:
Решить неравенство:
1) 3(3х - 1) > 10x - 14
9x - 3 > 10x - 14
9x - 10x > -14 + 3
-x > -11
x < 11 Знак неравенства меняется на противоположный при делении на -1.
Решение неравенства х∈(-∞; 11). ответ 1).
Неравенство строгое, скобки круглые.
2) 6 - 3х > 19 - (x - 7)
6 - 3х > 19 - х + 7
6 - 3х > 26 - х
-3х + х > 26 - 6
-2х > 20
2х < -20 Знак неравенства меняется на противоположный при делении на -1.
х < -10
Решение неравенства х < -10. ответ 3).
Неравенство строгое, скобки круглые.
3) x + 4 >= 4x - 5
x - 4x >= -5 - 4
-3x >= -9
3x <= 9 Знак неравенства меняется на противоположный при делении на -1.
x <= 3.
Решение неравенства х∈(-∞; 3]
Неравенство нестрогое, скобка квадратная, значение х=3 входит в интервал решений неравенства.
На числовой прямой такое значение отмечается заштрихованным кружком. ответ 4).
4) 6х - 15 > 8х - 11
6х - 8х > -11 + 15
-2х > 4
2х < -4 Знак неравенства меняется на противоположный при делении на -1.
х < -2
Решение неравенства х∈(-∞; -2). ответ 1).
Неравенство строгое, скобки круглые.