Отцу 35, а дочери 8.
Пошаговое объяснение:
Пусть x лет отцу, а y лет дочери. Тогда x - y = 27 (по условию задачи). Также известно, что если возраст отца увеличить в 3 раза, а возраст дочери увеличить 5 раз, то сумма их возрастов составит 145 лет. Тогда можно сказать, что 3x + 5y = 145. Объеденив два получившихся уравнения, получим систему:
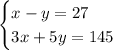
В первом уравнении выразим переменную x через y: x - y = 27 ; x = 27 + y. Подставим получившееся значение переменной x во второе уравнение: 3 · (27 + y) + 5y = 145 ; 81 + 3y + 5y = 145 ; 8y = 145 - 81 ; 8y = 64; y = 64 / 8 ; y = 8. Значит дочери 8 лет. Подставим уже известое значение y в уравнение x = 27 + y: x = 27 + 8 ; x = 35. Значит 35 лет отцу.
Пошаговое объяснение:
Пусть на рисунке а высота ленты - х см, а так как высот 4, то имеем - 4х см, тогда длина основания - у см, а так как их тоже 4 то имеем 4у см Длина обёрточной ленты равна 230 см. ,если обернуть коробку, как на рисунке a, то не хватит 10 см, отсюда получим, что сумма этих длин равна 4x + 4y=230 + 10
На рисунке b высота ленты - х см, а так как высот 2, то имеем - 2х см, тогда длина основания - у см, а так как их 6 то имеем 6у см Длина обёрточной ленты равна 230 см. если обернуть коробку, как на рисунке b, то на завязывание банта останется 30 см отсюда получим, что сумма этих длин равна 2x + 6y=230 - 30
Составим систему уравнений
{4x+4y=230+10 | :4
{2x+6y=230−30
x+y=60
х= 60 -у
Подставим во второе уравнение
2(60-у)+6у=200
120-2у+6у= 200
4у= 80
у= 20 см длина стороны основания коробки
х+20=60
х= 60-20
х= 40 см высота коробки
//////////////////////////