Есть несколько решения задачи.
Самый лёгкий - использовать формулу длины медианы равнобедренного треугольника.
m = (1/2)√(2a² + b²), где а - основание, b - боковая сторона.
Отсюда находим b = √(4m² - 2a²) = √(4*25 - 2*32) = √36 = 6.
ответ: длина боковых сторон равна 6.
Второй использование свойства деления медиан точкой пересечения 2 : 1 считая от вершины.
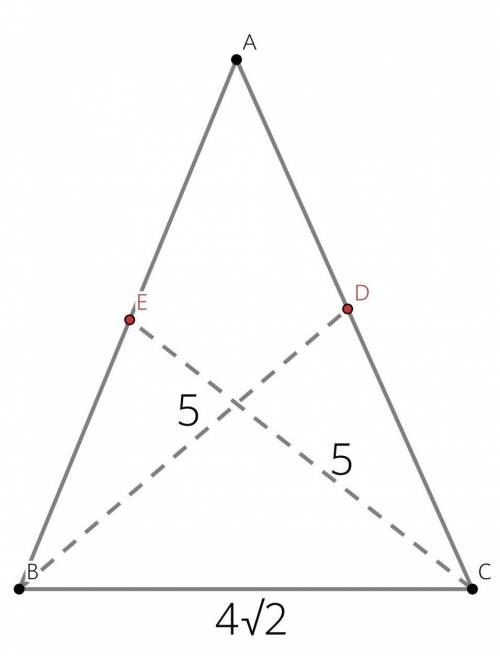
Пусть ВС - основание, О точка пересечения.
Находим косинус угла ОВС: (4√2/2)/(5/3) = 3√2/5.
По теореме косинусов находим ВЕ - половину боковой стороны.
ВЕ = √(25 + 8 - 2*5*(2√2)*(3√2/5)) = √(33 - 24) = √9 = 3.
Сторона равна 2*3 = 6.
Третий найти высоту треугольника к основанию по её третьей части и по Пифагору находим боковую сторону.
1)5х-4=6х+12,
5х-6х=4+12;
-х=16 |×(-1);
х=-16.
2)-10а-8=-9а+2,
-10а+9а=8+2;
-a=10 |×(-1);
a=10.
3)7m+1=2m-9,
7m-2m=-9-1;
5m=-10;
m=-2.
4)11m-3=-12-3(тут ты не поставил(а) букву,ниже напишу оба варианта,и ты выбери один - где стоит твоя буква)
11m-3=-12m-3,
11m+12m=-3+3;
23m=0;
m=0.
11m-3=-12-3m,
11m+3m=-12+3;
14m=-9;
m=-9/14(дробь).
5)6-24y=10-25y,
-24y+25y=10-6;
y=4.
6)11+6z=12+5z,
6z-5z=12-11;
z=1.
7)4a-3=7+5a,
4a-5a=7+3;
-a=10 |×(-1);
a=-10.
8)8+2c=6-3c,
2c+3c=6-8;
5c=-2;
c=-2/5(дробь).
9)3-11у=23-1у,
-11у+1у=23-3;
-10у=20;
у=-2.
10)5х-19=-2х+16,
5х+2х=16+19;
7х=25;
х=25/7(дробь).
x:2=20:4
x:2=5
x=5*2
x=10
10-10