Для того, чтобы представить в виде многочлена выражение (5 + 2y)(y^2 + 2y - 3) мы прежде всего выполним умножения многочлена на многочлен.
Итак, выполняем умножения и получаем выражение равносильное заданному:
(5 - 2y)(y^2 + 2y - 3) = 5 * y^2 + 5 * 2y - 5 * 3 - 2y * y^2 - 2y * 2y + 2y * 3 = 5y^2 + 10y - 15 - 2y^3 - 4y^2 + 6y.
Нам теперь нужно выполнить группировку и приведение подобных слагаемых в полученном выражении:
5y^2 + 10y - 15 - 2y^3 - 4y^2 + 6y = -2y^3 + 5y^2 - 4y^2 + 10y + 6y - 15 = 3y^2 - 4y^2 + 16y -15.
а)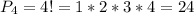
б)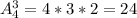
в) Цифры могут повторяться - тогда первая одна из 3 (кроме 0) вторая и третья любая из 4. Имеем 3*4*4=48
г) Не повторяются - тогда первая одна из 3, вторая одна из 3 оставшихся, третяя одна из 2 оставшихся т.е. 3*3*2=18