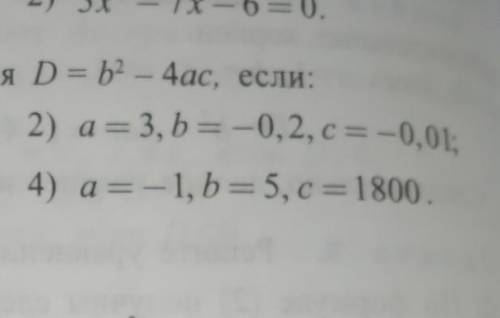
Сприйняття минулого з часом мимоволі змінюється. З одного боку, ми стаємо менш залежними від тих, хто "робив історію", ставав її героями чи антигероями, все менше маємо до них "сентиментів". Значно важливішими для нас стають джерела, яких історики відкривають дедалі більше, або аналізують у ширшому контексті.
З другого боку, час невпинно поглиблює прірву між нами та історичною минувшиною. Ця неуникнена дистанція провокує до того, що історики називають модернізацією.
Модернізація в історії становить чи не найбільший бар'єр для розуміння минулого. Це коли на речі та явища далекої минувшини ми дивимося очима людини з сучасним життєвим та освітнім досвідом - немотивовано переносимо цілком сучасні мисленневі практики та стереотипи на інші епохи.
Квадратным трёхчленом называется многочлен 2-ой степени, то есть выражение вида ax2 + bx + c, где a ≠ 0, b, c - (обычно заданные) действительные числа, называемые его коэффициентами, x - переменная величина.
Обратите внимание: коэффициент a может быть любым действительным числом, кроме нуля. Действительно, если a = 0, то ax2 + bx + c = 0·x2 + bx + c = 0 + bx + c = bx + c. В этом случае в выражении не остаётся квадрата, поэтому его нельзя считать квадратным трёхчленом. Однако, такие выражения-двучлены как, например, 3x2 − 2x или x2 + 5 можно рассматривать как квадратные трёхчлены, если дополнить их недостающими одночленами с нулевыми коэффициентами: 3x2 − 2x = 3x2 − 2x + 0 и x2 + 5 = x2 + 0x + 5.
Если стоит задача, определить значения переменной х, при которых квадратный трёхчлен принимает нулевые значения, т.е. ax2 + bx + c = 0, то имеем квадратное уравнение.
Если существуют действительные корни x1 и x2 некоторого квадратного уравнения, то соответствующий трёхчлен можно разложить на линейные множители: ax2 + bx + c = a(x − x1)(x − x2)
Замечание: Если квадратный трёхчлен рассматривать на множестве комплексных чисел С, которое, возможно, вы еще не изучали, то на линейные множители его можно разложить всегда.
Когда стоит другая задача, определить все значения, которые может принимать результат вычисления квадратного трёхчлена при различных значениях переменной х, т.е. определить y из выражения y = ax2 + bx + c, то имеем дело с квадратичной функцией.
При этом корни квадратного уравнения являются нулями квадратичной функции.
Квадратный трёхчлен также можно представить в виде
Решение прикреплено. Надеюсь, что всё понятно.