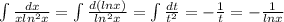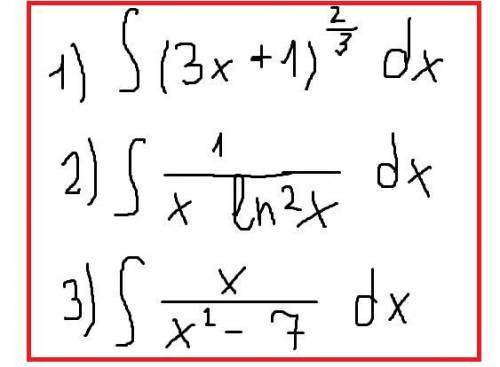
Пошаговое объяснение:
1)
\begin{gathered}\int\limits {(3x+1)^{\frac{2}{3} }} \, dx =\frac{1}{3}\int\limits {t}^{\frac{2}{3} } \, dt=\\=\frac{1}{3}*\frac{t^{\frac{2}{3} +1}}{\frac{2}{3} +1}= \frac{1}{3}* \frac{3}{5}t^{\frac{5}{3}}=\frac{1}{5}*(3x+1)^{\frac{5}{3}}\\3x+1=t; 3dx=dt; \\dx=\frac{1}{3}dt\end{gathered}
∫(3x+1)
3
2
dx=
3
1
∫t
3
2
dt=
=
3
1
∗
3
2
+1
t
3
2
+1
=
3
1
∗
5
3
t
3
5
=
5
1
∗(3x+1)
3
5
3x+1=t;3dx=dt;
dx=
3
1
dt
2)\int \frac{dx}{xln^2x}=\int \frac{d(lnx)}{ln^2x}=\int \frac{dt}{t^2}=-\frac{1}{t}=-\frac{1}{lnx}∫
xln
2
x
dx
=∫
ln
2
x
d(lnx)
=∫
t
2
dt
=−
t
1
=−
lnx
1
ответ: 4476°
Пошаговое объяснение:
Задание звучит так: Рассчитайте угол, на который вращается минутная стрелка между 12 a.m. (полднем) и 12.26 p.m (после полуночи)
1) За один час минутная стрелка делает полный оборот (с положения на 12 часов до положения на 12 часов)
Значит за 1 час минутная стрелка вращается на 360°
С полудня до полуночи проходил 12 часов
Значит за 12 часов минутная стрелка вращается на:
12×360 = 4320°
2) Теперь нужно посчитать, на какой угол стрелка вращается с полуночи (12 p.m) до 12.26 p.m
Полный оборот стрелки на часах - 360°
На часах есть 60 делений (каждое отвечает за 1 минуту)
Значит цена одного деления:
360÷60 = 6°
Тобишь за одну минуту минутная стрелка поворачивается на 6°
А за 26 минут:
6×26 = 156°
3) Значит за 12 часов 26 минут, минутная стрелка вращается на:
4320 + 156 = 4476°
Пошаговое объяснение:
1)
2)