1) Пусть уроков было N. Пусть Петя победил a раз, Коля b раз, Вася c раз.
Пусть Петя пропустил 1 урок, то есть был на N-1 уроке. Тогда:
Петя получил 4a + 1*(N-1-a) = N + 3a - 1 = 29 конфет.
Коля получил 4b + 1*(N-b) = N + 3b = 32 конфеты
Вася получил 4c + 1*(N-c) = N + 3c = 37 конфет
Из 1 уравнения получаем:
N + 3a = 30, N = 30 - 3a = 3(10 - a), то есть N кратно 3.
Тогда N - 3b и N - 3c тоже были бы кратны 3, но этого нет.
Значит, урок пропустил НЕ Петя.
Пусть урок пропустил Коля. Тогда получится:
Петя получил 4a + 1*(N-a) = N + 3a = 29 конфет.
Коля получил 4b + 1*(N-1-b) = N + 3b - 1 = 32 конфеты
Вася получил 4c + 1*(N-c) = N + 3c = 37 конфет
Тогда из 2 уравнения N + 3b = 33; N = 33 - 3b = 3(11 - b).
Получаем тоже самое: из 2 уравнения N кратно 3, а из 1 и 3 - нет.
Значит, урок пропустил Вася.
Петя получил 4a + 1*(N-a) = N + 3a = 29 конфет.
Коля получил 4b + 1*(N-b) = N + 3b = 32 конфеты
Вася получил 4c + 1*(N-1-c) = N + 3c - 1 = 37 конфет
Теперь из 3 уравнения: N = 38 - 3c, N на 3 не делится, все сходится.
Если написать 4 уравнение: a + b + c = N, то получаем систему:
{ N + 3a = 29
{ N + 3b = 32
{ N + 3c = 38
{ a + b + c = N
Но из этой системы получается N = 99/6 = 16,5, что невозможно.
Так что в задаче ошибка, но тем не менее
ответ: урок пропустил Вася.
2) Я не знаю, как это доказать, с геометрией у меня сложности.
3) Это намного проще, чем 1)
494 = 2*13*19 = 13*38
Это число 138.
12.
Дано:
квадрат;
P=12см;
Найти: d
1)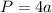 =>
=> 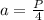 =>
=> 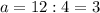
2) По т. Пифагора
ответ: 3√2 см
13.
Дано:
прямоугольник;
Найти: d
По т. Пифагора
ответ: 20 см
14.
Дано:
n-угольник;
Найти: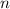
ответ: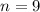
16.
Дано:
12-угольник;
Найти: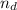
ответ: 54
17.
Дано:
ромб;
Найти: S
Площадь ромба равна половине произведения его диагоналей.
18/
Дано:
параллелограмм;
∠1+∠2+∠3=220°
Найти: меньший угол
Решение
1) ∠1+∠2+∠3+∠4=360°
∠4=360°-220°=140° - это смежный с меньшим
2) 180°-140°=40° - меньший
ответ: 40°
19)
Всего (n+3) вершин
ответ: 10
20)
Дано:
трапеция;
h=8 см;
a=4 см;
b=12 см
Найти: S
Решение
ответ: 64 см²