№829
1)Для каждого выражения под модулем уравнении допускаем случаи, когда соотв. выражение: ≥0 или <0, решаем получившиеся уравнения:
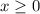
или:
0≤x/\x<∞
Получаем уравнение:
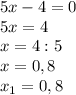
x<0
Получаем уравнение:
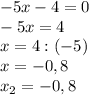
2)x≥0
Получаем уравнение:
17x/10-51/10=0 |*10
17X-51=0
17x=51
x=51:17
x=3
x1=3
x<0
Получаем уравнение:
-17x/10-51/10=0 |*10
-17x-51=0
-17x=51
x=51:(-17)
x= -3
x2= -3
3)y≥0
Получаем уравнение:
15y/2-15=0 | *2
15y-30=0
15y=30
y=30:15
y=2
y1=2
y<0
Получаем уравнение:
-15y/2-15=0 | *2
-15y-30=0
-15y=30
y=30:(-15)
y= -2
y2= -2
Пошаговое объяснение:
![x=(-inf;-\frac{2}{3}] и (3;inf)](/tpl/images/2082/4945/94b9e.png)
(inf заменяй на бесконечность)
Пошаговое объяснение:
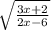
Чтобы выражение существовало нужно чтобы:
Знаменатель был не равен нулю и
Подкоренное выражение было не меньше нуля.
Остальных условий существования для данного выражения нет.
Чтобы знаменатель не был равен нулю,  не должно быть равно нулю.
не должно быть равно нулю.
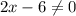
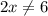
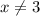
Значит  не равно нулю.
не равно нулю.
Следующее условие:
Чтобы подкоренное выражение не было меньше нуля, 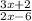 не должно быть меньше нуля.
не должно быть меньше нуля.
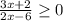
![x=(-inf;-\frac{2}{3}] и (3;inf)](/tpl/images/2082/4945/94b9e.png)
(inf заменяй на бесконечность)
Находим те значения, которые НЕ походят
![x\neq (-\frac{2}{3};3]](/tpl/images/2082/4945/483b6.png)
В итоге мы получили, что ![x\neq (-\frac{2}{3};3]](/tpl/images/2082/4945/483b6.png)
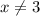 Второе высказывание, что
Второе высказывание, что 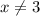 писать не нужно, так как из первого высказывания
писать не нужно, так как из первого высказывания ![x\neq (-\frac{2}{3};3]](/tpl/images/2082/4945/483b6.png) это и так понятно.
это и так понятно.
Теперь из ![x\neq (-\frac{2}{3};3]](/tpl/images/2082/4945/483b6.png) можно понять, что
можно понять, что ![x=(-inf;-\frac{2}{3}] и (3;inf)](/tpl/images/2082/4945/94b9e.png) .
.
7 гривен и 5 гривен.
Пошаговое объяснение:
Пусть в первом кармане х гривен, а во втором - у гривен.
По условию
{х - 1 = у + 1;
{(у - 1)•2 = х + 1;
{х - у = 2;
{(у - 1)•2 = х + 1;
{х = 2 + у;
{2у - 2 = х + 1;
{х = 2 + у;
{2у - 2 = 2 + у + 1;
{х = 2 + у;
{2у - у = 3 + 2;
{х = 2 + у;
{у = 5;
{х = 7;
{у = 5;
ответ: 7 гривен и 5 гривен.