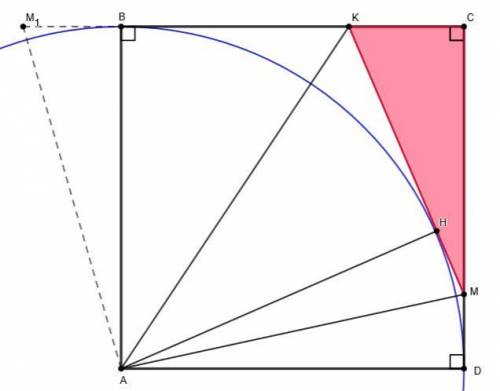
Условие: На сторонах ВС и CD квадрата ABCD взяли точки K и M так, что ∠MAK = 45°. Известно, что KM = 13 ,KC = 5 ,CM = 12. Найдите сторону квадрата ABCD.
Дано: K ∈ BC, M ∈ CD, ∠MAK = 45°, KM = 13 ,KC = 5 ,CM = 12.
Найти: BC.
Осуществим поворот ΔAMD на 90° против часовой стрелки ⇒ ΔAMD переходит в ΔAM₁B, ΔAMD = ΔAM₁B.
∠BAD = ∠BAK + ∠MAK + ∠MAD = 90° ⇒ ∠BAK + ∠MAD = 90° - ∠MAK = 90° - 45° = 45°
Из равенства ΔAMD = ΔAM₁B следует, что ∠MAD = ∠BAM₁, значит, ∠BAK + ∠BAM₁ = 45°.
ΔMAK = ΔM₁AK по двум сторонам и углу между ними:
AM = AM₁ - так как ΔAMD = ΔAM₁BАК - общая сторона∠MAK = ∠M₁AK = 45°Отсюда следует, что ∠АКМ = АКМ₁.
Аналогичным образом, осуществив поворот ΔAВК на 90° по часовой стрелке, можно утверждать, что ∠AMK = ∠AMD.
Заметим, что биссектрисы АК и АМ внешних углов при вершинах К и М ΔКСМ пересекаются в точке А, то есть точка А является центром вневписанной окружности ΔКСМ ⇒ AB = AD = AH - радиусы вневписанной окружности.
КВ = КН, MD = MH - как отрезки касательныхBC + СD = (BK + CK) + (CM + MD) = (KH + CK) + (CM + MH) = CK + CM + (KH + MH) = CK + CM + MK = 5 + 12 + 13 = 30
BC + СD = 30 ⇒ BC + BC = 30 ⇒ BC = 15
ответ: 15.
1)32:4=8
ответ: за одну ручку заплатили 8 рублей
Номер 2
1)28:7=4
ответ:ученики разбились на 8 команд
Номер 3
1)48:6=8
ответ: всего было 8 столов
Номер 4
1)12:3=4
ответ:у каждой сестры по 4 мелка
Номер 5
1)25:5=5
ответ:ткань разрезали на 5 частей
Номер 6
1)27:3=9
ответ: по 9 парт вымыл каждый
Номер 7
1)36:4=9
ответ:у каждого по 9 конфет
Номер 1
1)15:3=5 лотков с пирожками во второй день
2)15+5=20
ответ: всего привезли 20 лотков с пирожками
Номер 2
1)7*5=35 подосиновиков
2)7+35=42
ответ: всего грибник нашел 42 гриба
Номер 3
1)3*4=12 примеров
2)3+12=15
ответ:всего 15 заданий
Номер 4
1)7*3=21
2)7+21=28
ответ: всего 28 деревьев
Номер 5
1)42:6=7
2) 7+42=49
ответ: всего 49 машин
Номер 6
1)36:6=6
2)36+6=42
ответ:всего 42 дома
Номер 7
1)5*3=15
2)5+15=20
ответ:20 км от деревни до озера
Номер 8
1)40:4=10
2)40+10=50
ответ:всего 50 кг яблок собрали