:синей краски хватает на покраску квадрата со стороной 4 м. какой максимальной ширины прямоугольника можно закрасить этой краской , если его длина 20 дм. ( решение уравнением)

👇

Увидеть ответ

Ответ:

nikita71140

09.07.2022

S кв=4*4=16 м2

пусть х м ширина прямоугольника, длина 20 дм=0,2 м

х*0,2=16

х=16/0,2

х=80 м максимальная ширина прямоуг-ка, который можно закрасить имеющейся краской

4,7(78 оценок)

Открыть все ответы

Ответ:

026k

09.07.2022

Пошаговое объяснение:

рассматриваем два случая, т.к. модуль можно раскрыть с плюсом и с минусом

у вас рассмотрен первый случай, когда модель раскрывают с минусом

|-x| = 6, |x| = 6

|-(|x| - 2)| = 6 - так же верно, отсюда минус

-(|x| - 2) = 6

далее раскрывая скобки получаем запись аналогичную:

(-1) * (|x| - 2)

умножаем (-1) на каждое слагаемое:

(-1) * |x| + (-1) * (-2) = -|x| + 2

так же можно просто запомнить правило:

при умножении на "-" меняем все знаки на противоположные

заметьте, у нас был в скобках |x| стал -|x|, было -2 стало +2

дальнейшее решение:

-|x| + 2 = 6

-|x| = 6 - 2

-|x| = 4

|x| = -4

нет решений, т.к. модуль не может быть отрицательным

рассматриваем второй случай, про который говорили в начале

|x| - 2 = 6

|x| = 6 + 2

|x| = 8

x = -8 или x = 8

4,7(65 оценок)

Ответ:

Kate7779393727

09.07.2022

Событие B состоит в том, что детали извлечены из 2-й партии

Рассмотрим гипотезы A₁, A₂, A₃, которые состоят из следующих событий

A₁ — детали извлекались из первой партии;

A₂ — детали извлекались из второй партии;

A₃ — детали извлекались из третьей партии.

Вероятность достать детали в каждой партии из трех равна 1/3, т.е.

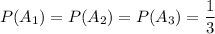
$P(A_1)=P(A_2)=P(A_3)=\dfrac{1}{3}$

Условная вероятность 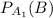$P_{A_1}(B)$ равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.

Условная вероятность 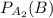$P_{A_2}(B)$ , равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.

Условная вероятность 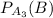$P_{A_3}(B)$ , равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.

Вероятность того, что деталь извлечена из второй партии, (по формуле Байеса), равна:

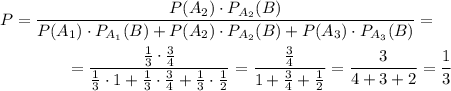
$P=\dfrac{P(A_2)\cdot P_{A_2}(B)}{P(A_1)\cdot P_{A_1}(B)+P(A_2)\cdot P_{A_2}(B)+P(A_3)\cdot P_{A_3}(B)}=\\ \\~~~~~~~~~~~~~=\dfrac{\frac{1}{3}\cdot\frac{3}{4}}{\frac{1}{3}\cdot 1+\frac{1}{3}\cdot\frac{3}{4}+\frac{1}{3}\cdot\frac{1}{2}}=\dfrac{\frac{3}{4}}{1+\frac{3}{4}+\frac{1}{2}}=\dfrac{3}{4+3+2}=\dfrac{1}{3}$