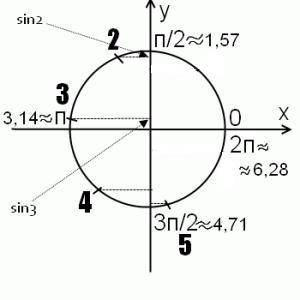
Единичная окружность понять, чему равны sin 2, sin 3, sin 4, sin5.
1 радиан - это угол, длина дуги которого равна радиусу окружности. Соответственно, определяем приблизительное местонахождение на единичной окружности углов в 2, 3, 4, и 5 радиан, отмечая каждую следующую точку через дугу, длина которой равна радиусу.
Поскольку синус - это ордината соответствующей точки на единичной окружности, то для нахождения sin 2, sin 3, sin 4, sin 5 достаточно определить значение y в точках 2, 3, 4, 5 радиан.
Поскольку синус — это y, то вверху, над осью x, синус принимает положительные значения. Поэтому sin 1>0, sin 2>0, sin 3>0. Соответственно внизу синус отрицателен: sin 4<0, sin 5<0.
ответ: Наибольшее sin 2
8.61+(-(3.99-2.65))=8.61-(3.99-2.65)=8.61-1.34=7.27
ответ: б)7.27
при x=-2.34, то (-x)+(-1.09)+5.26=2.34-1.09+5.26=6.51
г) другой ответ
найдите сумму всех целых чисел от -16 до 13
-16+(-15)+..+12+13=-16-15-14+(13-13)+(12-12)+...+(1-1)+0=-45
б)-45
.решите уравнение: у - (-2целых 3/4)=-2.33
у +2.75=-2.33
y=-2.33-2.75
y=-5.08=-5 целых 2/25
ответ: б)-5цел.2/25
найдите сумму всех целых отрицательных чисел больших -8 ,но меньших -3.
-7+(-6)+(-5)+(-4)+(-3)+(-2)+(-1)+0+1+2=-25
г)другой ответ
кажись так
Обозначим стороны тр-ка a, a и b и составим систему
a^2 * b = 64
2a + b= 12
b = 12 - 2a
a^2 * (12 - 2a) = 64
12a^2 - 2a^3 - 64 = 0
a^3 - 6a^2 + 32 =0
перебираем делители свободного члена и находим среди них тот, который обращает в ноль левую часть. это число -2
Т.о. кубический многочлен делится на a+2
частное от деления многочлена на двучлен равно a^2 - 8a + 16
решаем уравнение a^2 - 8a + 16 = 0
D = 64 - 64 = 0 a = 8/2 = 4
Кубическое уравнение имеет 3 корня -2, 4, 4, из которых подходит a = 4
b = 12 - 2*4 = 4
Получается равносторонний тр-к со стороной 4
Проверка : 4*4*4 = 64 P = 4+4+4 =12