Событие B состоит в том, что детали извлечены из 2-й партии
Рассмотрим гипотезы A₁, A₂, A₃, которые состоят из следующих событий
A₁ — детали извлекались из первой партии;
A₂ — детали извлекались из второй партии;
A₃ — детали извлекались из третьей партии.
Вероятность достать детали в каждой партии из трех равна 1/3, т.е.
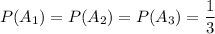
Условная вероятность 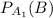 равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
равна 1, так как это событие достоверно, так как в первой партии все детали стандартны.
Условная вероятность 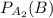 , равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
, равна 15/20 = 3/4 — вероятность того, что из второй партии извлечена стандартная деталь.
Условная вероятность 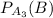 , равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
, равна 10/20 = 1/2 — вероятность того, что из третьей партии извлечена стандартная деталь.
Вероятность того, что деталь извлечена из второй партии, (по формуле Байеса), равна:
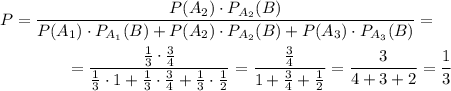
ответ: 1/3.
Рассмотрим число 13. Его можно использовать не более 4 раз, т.к. 5-й раз его можно заменить на тринадцать чисел 5.
Значит при только 13 мы можем получить числа
13
26
39
52
Далее для представления чисел в виде суммы уже можно пользоваться полученными числами и числом 5, т.к. при прибавлении 5 к любому числу выше можно получить число с любой последней цифрой. Т.е. остальные числа можно представить в виде суммы слагаемых, которые равны либо 5 либо 13.
Посмотрим, какое из чисел меньше 52 еще нельзя представить в таком виде. Не получится представить число, заканчивающееся на цифру 7, т.к. цифру 7 мы можем получить, только прибавив 5 к 52, т.е. использовав число 13 четыре раза. Поэтому число 47 является наибольшим, которое нельзя представить в нужном виде.
Как то так...