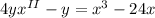
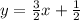или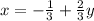 
Пошаговое объяснение:
Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).
Решать задачу будем следующим образом:
вспомним формулу для нахождения расстояния между точками на плоскости;
обозначим точки равноудаленные от А и В координатами (x; y);
запишем расстояния между точкой А и (x; y);
запишем расстояние между точками B и (x; y);
приравняем расстояния и выразим одну переменную через другую.
Вспомним формулу для нахождения расстояния на плоскости
Формула для нахождения расстояния между точками на плоскости выглядит так:
AB =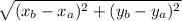 
, где точки А и В заданы координатами A и B
Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).
Составим уравнение геометрического места точек
Записываем расстояние между точкой A (2; -3) и (x; y):
;
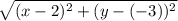Записываем расстояние между точками B (-4; 1) и (x; y):
;
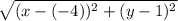Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:
;
;
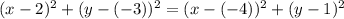Открываем скобки, переносим все слагаемые в право и приводим подобные.
;
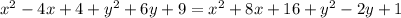
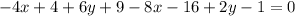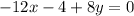
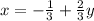
или
.
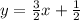(см. объяснение)
Пошаговое объяснение:
Рассмотрим сначала первое неравенство системы:
Видно, что левая его часть должна быть положительна. В свою очередь числитель дроби положителен. Это означает, что неравенство может быть верным только, если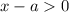
.
Тогда при домножении левой и правой частей неравенства на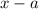
его знак сохранится.
Получим эквивалентную систему:
Преобразуем ее до более удобного вида:
(данного результата можно было добиться также и приведением дроби к общему знаменателю; рассматриванием двух случаев; исключением одного)
Построим решения всех неравенств записанной выше системы в координатах (x; a):
(см. прикрепленный файл | выделено синим)
Рассмотрим вторую строку системы:
Преобразуем ее:
Приведем систему к более удобному виду:
Построим решения всех неравенств записанной выше фразы в координатах (x; a):
(см. прикрепленный файл | выделено фиолетовым)
Будем двигать горизонтальную прямую до тех пор, пока не добьемся требуемого результата.
(см. прикрепленный файл | выделено оранжевым)
Тогда понятно, что достаточно решить систему:
Откуда следует, что при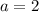
исходная система неравенств имеет единственное решение 
.
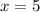Задание выполнено!