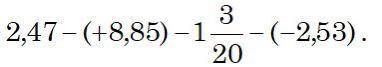
Пошаговое объяснение:
1. 1) 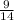 и
и 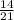 =
= 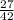 и
и 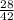 => 2-е больше 1-го. Сумма:
=> 2-е больше 1-го. Сумма: 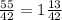 Разность:
Разность: 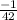 (или
(или 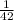
2) 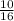 и
и 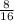 , 1-е больше.
, 1-е больше.
Сумма = 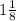 . Разность:
. Разность:  .
.
3) 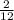 и
и 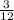 . 2-е больше. Сумма:
. 2-е больше. Сумма: 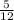 . Разность:
. Разность: 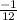 (или
(или 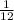
4) 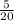 и
и 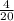 . 1-е больше. Сумма
. 1-е больше. Сумма 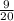 . Разность:
. Разность: 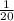
5) 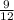
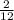 . 1-е больше. Сумма
. 1-е больше. Сумма 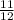 . Разность:
. Разность: 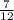
2. 1) 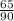 и
и 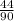 . 1-е больше. Сумма
. 1-е больше. Сумма 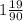 . Разность:
. Разность: 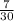 .
.
2) 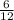 и
и 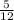 . 1-е больше. Сумма:
. 1-е больше. Сумма: 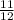 . Разность:
. Разность: 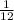
3) 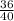 и
и 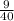 . 1-е больше. Сумма:
. 1-е больше. Сумма: 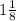 . Разность:
. Разность: 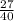
4) 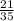 и
и 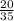 . 1-е больше. Сумма:
. 1-е больше. Сумма: 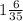 . Разность
. Разность 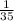 .
.
5) 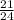 и
и 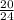 . 1-е больше. Сумма:
. 1-е больше. Сумма: 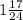 Разность:
Разность: 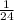 .
.
3. 1) 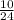 и
и 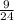 . 1-е больше. Сумма:
. 1-е больше. Сумма: 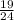 . Разность
. Разность 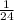 .
.
2) 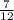 и
и 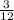 . 1-е больше. Сумма:
. 1-е больше. Сумма: 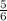 . Разность
. Разность 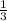 .
.
3) 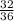 и
и 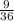 . 1-е больше. Сумма:
. 1-е больше. Сумма:
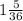 . Разность:
. Разность: 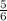 .
.
4) 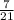 и
и 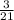 . 1-е больше. Сумма:
. 1-е больше. Сумма: 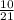 . Разность
. Разность 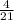 .
.
5) 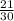 и
и 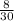 . 1-е больше. Сумма:
. 1-е больше. Сумма: 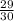 . Разность
. Разность 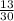 .
.
ответ: π/12 единиц кубических.
Пошаговое объяснение:
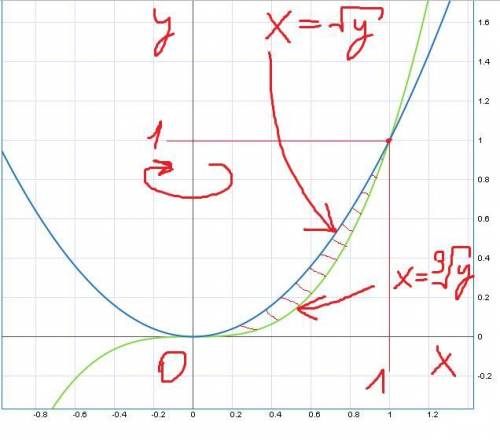
Построим графики (рисунок 1).
Так как полученная фигура крутиться вокруг оси оу, выведем x из уравнений кривых:
![y=x^{2} = x=\sqrt[2]{y} \\y=x^{3} = x=\sqrt[3]{y}](/tpl/images/0128/6284/431d4.png)
Теперь найдём объём тела вращения. Делаем следующее:
1) Так как график ![x=\sqrt[3]{y}](/tpl/images/0128/6284/27428.png) правее чем
правее чем 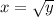 , то в интеграле отнимем правый график от левого графика.
, то в интеграле отнимем правый график от левого графика.
2) Так как график по оси оу находиться в диапазоне [0; 1], то и пределы интегрирования будут соответствующие.
3) По формуле 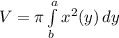 найдём объём, учитывая, что надо отнять правый график функции от левого.
найдём объём, учитывая, что надо отнять правый график функции от левого.
Эти шаги видно в рисунке 2.
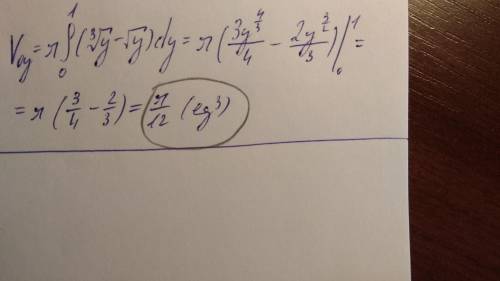
ответ: -5.
Пошаговое объяснение:
2,47-(+8,85)-11/20 - (-2,53)=
1) 2,47+(-8,85) = - 8,85 - 2,47 = - 6,38;
2) -6,38 - 1 3/20 = -(6,38 + 1,15) = - 7,53;
3) - 7,53 - (-2,53) = -7,53 + 2,53 = -(7,53 - 2,53)= -5