В решении.
Пошаговое объяснение:
Двигаясь против течения реки, теплоход за 5 ч расстояние в 120 км.
Найди скорость течения реки, если собственная скорость теплохода — 27 км/ч.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость течения реки.
27 - х - скорость теплохода против течения.
По условию задачи уравнение:
(27 - х) * 5 = 120
135 - 5х = 120
-5х = 120 - 135
-5х = -15
х = -15/-5
х = 3 (км/час) - скорость течения реки.
Проверка:
(27 - 3) * 5 = 120 (км), верно.
В решении.
Пошаговое объяснение:
Двигаясь против течения реки, теплоход за 5 ч расстояние в 120 км.
Найди скорость течения реки, если собственная скорость теплохода — 27 км/ч.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость течения реки.
27 - х - скорость теплохода против течения.
По условию задачи уравнение:
(27 - х) * 5 = 120
135 - 5х = 120
-5х = 120 - 135
-5х = -15
х = -15/-5
х = 3 (км/час) - скорость течения реки.
Проверка:
(27 - 3) * 5 = 120 (км), верно.
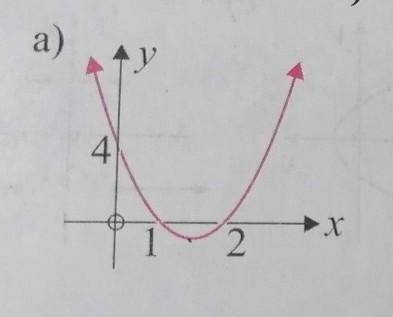
На рисунке видны корни: х1 = 1, х2 = 2 и точка пересечения оси Оу, ордината которой равна слагаемому "с" в уравнении параболы:
у = ах² + by + c, то есть, с = 4.
Ось параболы проходит посредине между корнями, хо = (1+2)/2 = 3/2.
Используем формулу: хо = -b/2a, отсюда находим зависимость: b = -3a.
Подставляем координаты корня параболы в уравнение:
0 = a*1² + (-3a)*1 + 4,
2a = 4, a = 4/2 = 2.
Отсюда b = -3*2 = -6.
ответ: y = 2x² - 6x + 4.