Рисунок во вложении.
Расставим на единичной окружности точки, соответствующие числам
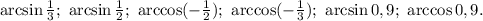
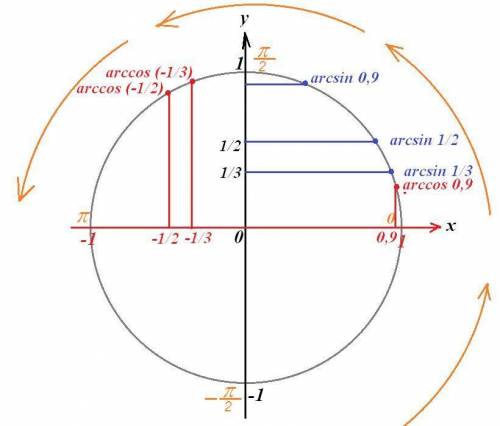
Точки расставлены в соответствии с определением величин arcsin t и arccos t. Принято во внимание, что 0 < arccos t < π и -π/2 < arcsin t < π/2, где t∈[-1; 1].
Теперь при движении по дуге окружности против часовой стрелки (положительное направление - указано стрелками) от числа 0 до числа π видно, что меньшее из чисел - это arccos 0,9, и большее из чисел - arccos (-1/2).
Таким образом, в порядке возрастания числа можно расположить так:
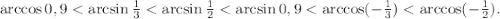
1)(3у+5):5+(9у-5):4=6+(3у+1):2
0,6у+1+2,25у-1,25=6+1,5у+0,5
2,85у-0,25=1,5у+6,5
2,85у-1,5у=6,5+0,25
1,35у=6,75
у=6,75/1,35
у=5
2)3/4+2х+5=2 3/4х+4,1+0,9
2х+5 3/4=2 3/4х+5
2х-2 3/4х=5-5 3/4
-3/4х=-3/4
х=-3/4:(-3/4)
х=1