
Пошаговое объяснение:
9x²+5y²+18x–30y+9=0
1. Определение типа кривой.
квадратичная форма
B = 9x² + 5y²
приводим к каноническому виду
матрица этой квадратичной формы:
9 0
0 5
собственные числа и собственные векторы этой матрицы
(9 - λ)*х₁+ 0y₁ = 0
0x₁ + (5 - λ)y₁ = 0
характеристическое уравнение
λ² - 14λ + 45 = 0 ⇒ λ₁ = 9; λ₂=5
λ₁ > 0; λ₂ > 0 - это эллипс
теперь надо выделить полные квадраты
для х
9(x²+2x + 1) -9= 9(x+1)²-9
и для у
5(y²-2*3y + 3²) -5*3² = 5(y-3)²-45
и получим
9(x+1)²+5(y-3)² = 45
делим на 45 и получаем каноническое уравнение эллипса
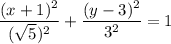
2) координаты фокусов, вершин и центра
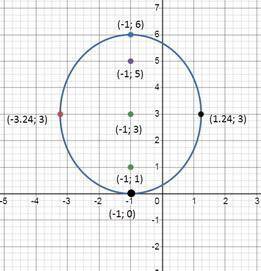
центр C(-1; 3)
полуоси
меньшая a = √5;
большая b= 9
координаты фокусов
F₁(-c;0) и F₂(c;0), где c - половина расстояния между фокусами
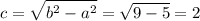
координаты фокусов F₁(-2;0) и F₂(2;0)
с учетом центра, координаты фокусов равны: F₁(-1;1) и F₂(-1;5)
вершины
х = -1; (у-3)²=9 ⇒ у₁ = 0, у₂ = 6
тогда вершины по оси оу (-1; 0) (-1; 6)
у= 3; (х+1)²=5 ⇒ х₁ = -1+√5 ≈1,24; х₂ = -1-√5 ≈ -3,24
и тогда вершины по оси ох (-1+√5; 3) (-1-√5; 3)
15 м
Пошаговое объяснение:
.
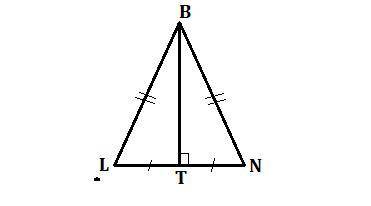
Составим систему уравнений.
P ΔLBN = LB + BN + LN
LB = BN, по свойству равнобедренного треугольника.
Пусть x м - LB и BN, тогда y м - LN
x + x + y = 50 - 1 уравнение
Составляем 2 уравнение:
P ΔLBT = LB + BT + LT
x м - LB
BT - высота, медиана, биссектриса (по свойству равнобедренного треугольника), значит LT = TN = 1/2LN
Тогда 1/2y м - LT
ΔLBT - прямоугольный, так как BT - высота
⇒ по теореме Пифагора:
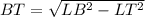
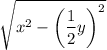 м - BT
м - BT
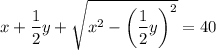 - 2 уравнение
- 2 уравнение
Решим получившуюся систему уравнений:
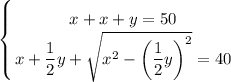
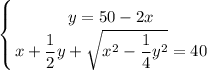
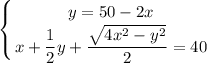
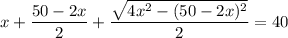
В числителе 2 дроби видим формулу сокращённого умножения - квадрат разности. Раскладываем по формуле: (a - b)² = a² - 2ab + b²
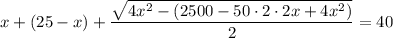
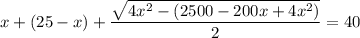
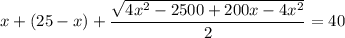
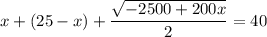
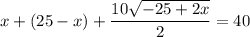
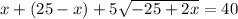
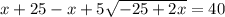
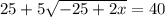
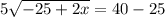
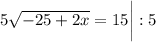
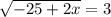
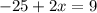
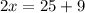
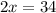
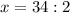
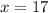
17 м - LB
17 + 17 + y = 50
y = 50 - 17 - 17
y = 50 - 34
y = 16
16 м - LN
LT = 1/2LN = 16/2 = 8 м
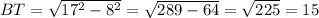 м
м
.
P ΔLBN = LB + LN + BN
Так как ΔLBN - равнобедренный ⇒ LB = BN (по свойству равнобедренного треугольника)
⇒ P ΔLBN = 2LB + LN
2LB + LN = 50 м
P ΔLBT = LB + BT + LT
Так как BT - медиана, по условию ⇒ LT = 1/2LN
⇒ P ΔLBT = LB + BT + 1/2LN
LB + BT + 1/2LN = 40 м | · 2
2LB + 2BT + LN = 80 м
Так как 2LB + LN = 50 м ⇒ 2BT = 80 - 50 = 30 м
⇒ BT = 30 : 2 = 15 м
пульт, тора, таро, порт