
а) Есть теорема: a/b < (a+1)/(b+1) при любых a > 0; b > 0; b > a
Для доказательства найдем разность через общий знаменатель:
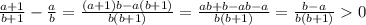
Конечная дробь больше 0, потому что числитель больше 0 (потому что b > a) и знаменатель тоже больше 0.
Если разность дробей больше 0, то первая дробь больше второй.
10/11 > 9/10 > 8/9.
Наибольшее 10/11.
б) 11/20 = 22/40 > 21/40
11/20 = 33/60 > 31/60.
Наибольшее 11/20
в) 23/48 = 24/48 - 1/48 = 1/2 - 1/48,
17/36 = 18/36 - 1/36 = 1/2 - 1/36
35/72 = 36/72 - 1/72 = 1/2 - 1/72.
Чем больше знаменатель, тем меньше дробь. 1/72 < 1/48 < 1/36
Чем меньше вычитают из числа 1/2, тем больше остается.
1/2 - 1/72 > 1/2 - 1/48 > 1/2 - 1/36
Наибольшее 35/72
а) Есть теорема: a/b < (a+1)/(b+1) при любых a > 0; b > 0; b > a
Для доказательства найдем разность через общий знаменатель:
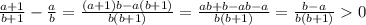
Конечная дробь больше 0, потому что числитель больше 0 (потому что b > a) и знаменатель тоже больше 0.
Если разность дробей больше 0, то первая дробь больше второй.
10/11 > 9/10 > 8/9.
Наибольшее 10/11.
б) 11/20 = 22/40 > 21/40
11/20 = 33/60 > 31/60.
Наибольшее 11/20
в) 23/48 = 24/48 - 1/48 = 1/2 - 1/48,
17/36 = 18/36 - 1/36 = 1/2 - 1/36
35/72 = 36/72 - 1/72 = 1/2 - 1/72.
Чем больше знаменатель, тем меньше дробь. 1/72 < 1/48 < 1/36
Чем меньше вычитают из числа 1/2, тем больше остается.
1/2 - 1/72 > 1/2 - 1/48 > 1/2 - 1/36
Наибольшее 35/72
ответ: 1. y=C*e^[cos(x)]+1; 2. y=1/3*√(2*x-1)-1; 3. y=e^(2*x)*[C1*cos(4*x)+C2*sin(4*x)]
Пошаговое объяснение:
1. Перепишем уравнение в виде y'+y*sin(x)-sin(x)=0. Это - ЛДУ 1 порядка, положим y=u*v. Тогда y'=u'*v+u*v' и уравнение примет вид: u'*v+u*v'+u*v*sin(x)-sin(x)=v*[u'+u*sin(x)]=u*v'-sin(x)=0. Так как одной из функций u или v мы можем распорядиться по произволу, то поступим так с u и потребуем, чтобы она удовлетворяла уравнению u'+u*sin(x)=0, или du/dx=-u*sin(x). Решая его, находим u=e^[cos(x)]. Подставляя это выражение в уравнение u*v'=sin(x), получаем уравнение v'=dv/dx=sin(x)*e^[-cos(x)]. Решая его, находим v=C+e^[-cos(x)], где C - произвольная постоянная. Отсюда y=u*v=C*e^[cos(x)]+1.
2. Данное уравнение можно переписать в виде dy/dx=(y+1)/(2*x-1), или dy/(y+1)=dx/(2*x-1). Интегрируя, находим ln/y+1/=1/2*ln/2*x-1/+1/2*ln/C/, где C - произвольная, но не равная нулю постоянная. Отсюда y=√[C*(2*x-1)]-1. Используя условие y(5)=0, получаем уравнение √(9*С)=1, откуда C=1/9. Тогда искомое частное решение y=1/3*√(2*x-1)-1.
3. Имеем однородное ЛДУ 2 порядка. Составляем характеристическое уравнение: k²-4*k+20=0. Оно имеет комплексные сопряжённые корни k1=2+4*i и k2=2-4*i, где i=√(-1). Поэтому общее решение уравнения таково: y=e^(2*x)*[C1*cos(4*x)+C2*sin(4*x)], где C1 и C2 - произвольные постоянные.