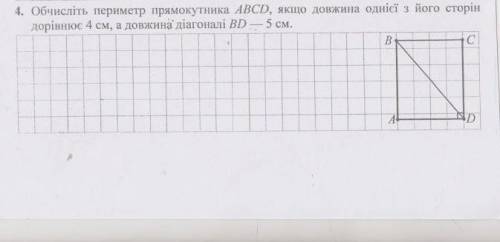
Дано: ABCD - прямоугольник
BA = CD = 4 см
BD = 5 см
Найти: P abcd
Теорема Пифагора ⇒ с² = a² + b² ( гипотенуза в квадрате равна сумме квадратов катетов )
Диагональ BD делит прямоугольник ABCD на два одинаковых прямоугольных треугольника
Я буду рассматривать треугольник ABD , но можно решать и по треугольнику BCD.
AB и AD два катета, а BD является гипотенузой
Решаем по формуле a² + b² = c², с которой находится гипотенуза прямоугольного треугольника , только немного изменим её чтобы можно было найти один из катетов ⇒ a² = c² - b²
BA = b ; AD = a ; BD = c
AD² = BD² - BA²
AD² = 5² - 4²
AD² = 25 - 16
AD² = 9
AD = √9
AD = 3 см
Периметр прямоугольника находится по формуле ⇒ P = 2 ( a + b ),
где a и b стороны прямоугольника
P abcd = 2 ( 4 + 3 ) = 2 · 7 = 14 см
ответ: Периметр прямоугольника равен 14 см
Пошаговое объяснение:
1) Пусть задуманное число х , тогда
(18*х)-73= 89
18х= 89+73
18х= 162
х= 162 : 18
х= 9- задуманное число
2) 2( b+5)+3 = 2b+10+3= 2b+13 при b=4
2*4+13= 12+13= 25
ответ : 25
3) 28 = 2*2*7
делителями числа будут его множители , их произведение , само число и 1
Делителями 28 будут числа : 1; 2; 4; 7; 14; 28
4) Разложением чисел 72 и 120 на простые множители являются простые множители этих чисел :
72 = 2*2*2*3*3
120 = 2*2*2*3*5
5) НОД ( 72 ; 120 ) = 2*2*2*3= 24
НОК ( 72 ; 120) = 2*2*2*3*3*5= 360
14
Пошаговое объяснение:
Пусть АВ = 4 , тогда
АВ^2 + AD^2 = BD^2
AD^2 = BD^2 - АВ^2
AD^2 = 25-16=9
AD = 3
P = AB + AD + CD + BC = 4+3+4+3 = 14