
Так как две стороны треугольника, по условию, равны, то треугольник АВС равнобедренный.
Тогда построим высоту ВН, которая так же будет медиана треугольника АВС, тогда АН = СН = АС / 2 = 5 / 2 = 2,5 см.
Определим по теореме Пифагора высоту ВН.
ВН2 = АВ2 – АН2 = 36 – 6,25 = 29,75.
ВН = √29,75 см.
Определим площадь треугольника АВС.
Sавс = АС * ВН / 2 = 5 * √29,75 / 2 = 2,5 * √29,75 см2.
Определим полупериметр треугольника.
р = (6 + 6 + 5) / 2 = 17 / 2 = 8,5 см.
Тогда радиус вписанной окружности равен:
R = Sавс / р = 2,5 * √29,75 / 8,5 ≈ 1,6 см.
ответ: Радиус вписанной окружности равен 1,6 см
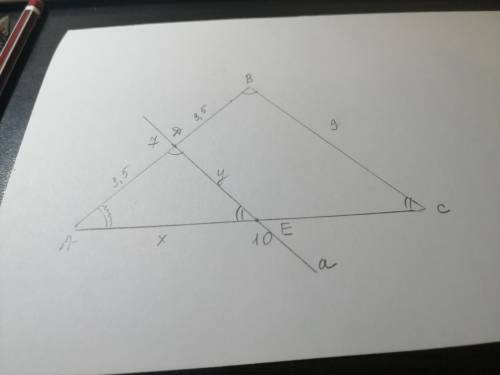
Сторона AD=3,5 см; сторона DE= 4,5 см; сторона АЕ=5 см
Пошаговое объяснение:
Два Δ называются подобными, если все ∠ одного треугольника соответственно равны ∠ другого треугольника, и все сходственные стороны этих треугольников пропорциональны.
1) Отложим точку D на стороне АВ так, чтобы АD=DB (по условию)
2) Проведем прямую а, отсекающую подобный Δ от данного. Для этого проведем через точку D прямую, ║стороне ВС и отметим точку Е.
3) ∠А -общий, ∠ АDE =∠ ABC (т к АВ-секущая двух параллельных прямых), а ∠ AED=∠АСВ
4) Обозначим сторону АЕ за х, а сторону DE за у.
5) Если в двух Δ углы при вершинах одного Δ соответственно равны углам при вершинах другого Δ, то соответственные стороны этих Δ связаны отношением: АВ/АD=АС/АЕ=ВС/DE. Подставляем известные значения:
2/1=10/х=9/у, откуда х=5, у=4,5
Сторона AD=3,5 см; сторона DE= 4,5 см; сторона АЕ=5 см
1)4x-3x>1-2
x>-1
2)2x-x>6-1
x>5
3) 6x-2x>9-1
4x>8
x>2