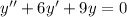
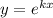 .
.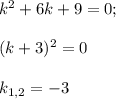
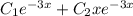
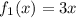 и
и 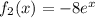
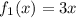
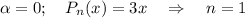
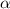 с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.
с корнями характеристического уравнения, и, принимая во внимания, что n=1, частное решение будем искать в виде.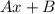
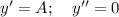 , подставим в исходное уравнение без функции
, подставим в исходное уравнение без функции 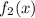 .
.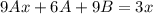
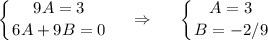
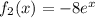
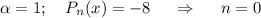
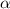 с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде:
с корнями характеристического уравнения и принимая во внимая, что n=0, частное решение будем искать в следующем виде: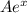
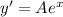 и
и 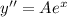
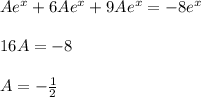
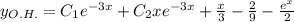
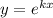 .
.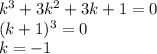
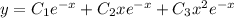
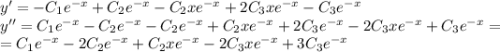
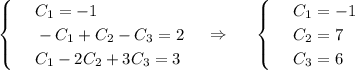
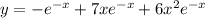
а) 2/13 від 52 кг 2/13*52=2/1*4=8
б) число , 17% якого становить 102.102/17*100=600
2) Розвязати рівняння:
3,7-2,6(х-3)=5(8-0,2х)
3,7-2,6х+7,8=40-х
11,5-2,6х=40-х
-2,6х+х=40-11,5
-1,6х=28,5
х=-28,5/1,6
х=17,8125
3) Першого дня туристи подолали 2/15 наміченого маршруту, а другого дня 1/6 наміченого маршруту. Після цього їм залишилося пройти половину маршруту і ще 12 км. Якою була довжина маршруту?
х-длина маршрута
2/15х+1/6х=1/2х-12
2/15х+1/6х-1/2х=-12
4/30х+5/30х-15/30х=-12
-6/30х=-12
-1/5х=-12
1/5х=12
х=12:1/5
х=12*5/1
х=60км
4) Знайти найбільше чотирицифрове число, кратне 53.
9999/53=188 и 35 в остатке
188*53=9964