Дано уравнение √(2x+4) = 1 - 2x.
ОДЗ: 2x + 4 ≥ 0, х ≥ -2,
1 - 2x ≥ 0, х ≤ 1/2.
Вывод: обе части его - положительны.
Левая часть - возрастающая функция, правая - убывающая.
Значит, есть одна точка пересечения, в которой справедливо равенство (если оно существует).
Возведём его в квадрат: 2x + 4 = 1 - 4x + 4x².
4x² - 6x - 3 = 0. Д = 36 + 4*4*3 = 84. √84 = 2√21.
х1 = (6 + 2√21)/8 = (3 + √21)/4 ≈ 1,89564. По ОДЗ не принимаем.
х2 = (6 - 2√21)/8 = (3 - √21)/4 ≈ -0,39564.
ответ: корень один и равен х = (3 - √21)/4 ≈ -0,39564.
ответ можно подтвердить графически: ведь корень - это точка пересечения двух графиков у = √(2x+4) и у = 1 - 2x.
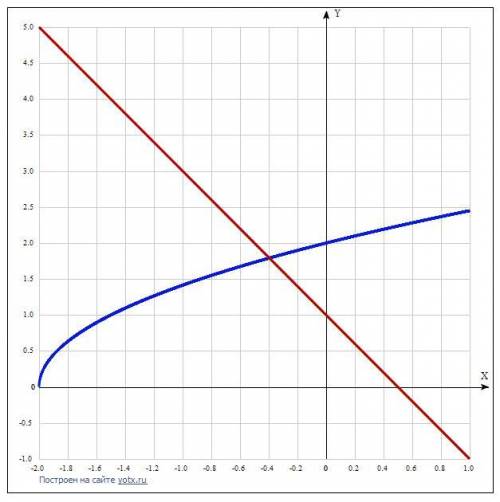
Пусть функция слева:
Вначале порассуждаем над графиками и свойствами функций.
1) Косинус - периодическая четная функция, период равен 2π.
2) y2 - это прямая, но за счет модуля "ломаная". Для того, чтобы построить эту функцию, необходимо вначале построить график функции
3) Теперь найдем интервал, на котором будут пересечения двух графиков. Известно, что
4) 8π для косинуса - это четыре периода. Значит, вправо от оси Оу будет 4 промежутка возрастания и 4 промежутка убывания. Аналогично влево от оси Оу. Итого: 16 промежутков ("кусочков" функции). Соответственно, прямая пересечет график косинуса в 16 точках.
Убедимся в полученном ответе, начертив графики функций: косинус - стандартная функция, ее общий вид необходимо знать; функция по модулю - уже расписано, как начертить. Оба графика чертим в одной координатной плоскости!
ответ: 16 решений