Сумма длины и ширины 42:2 = 21 см.
Пусть сторона квадрата x см.
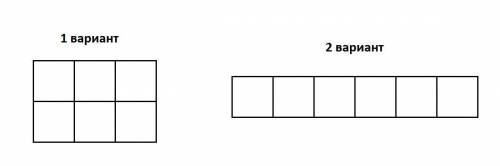
Есть два вариант, как могли разрезать прямоугольник на 6 одинаковых квадратов (см. рис.).
В первом случае одна сторона прямоугольника будет 2x см, другая 3x см.
2x+3x = 21
5x = 21
x = 4,2 см - сторона квадрата.
4,2·2 = 8,4 см одна сторона прямоугольника
4,2·3 = 12,6 см другая сторона прямоугольника.
8,4*12,6 = 105,84 см² площадь прямоугольника.
Во втором случае одна сторона прямоугольника будет x см, другая 6x см.
x+6x = 21
7x = 21
x = 3 см одна сторона прямоугольника
3*6 = 18 см другая сторона прямоугольника
3*18 = 54 см² площадь прямоугольника.
Катет a с высотой h образуют треугольник, подобный заданному.
Отношение h/a - это косинус угла (пусть А) между этим катетом и высотой, равный углу между вторым катетом и гипотенузой.
Находим синус угла: sin A = √(1 - (h/a)²) = √(a² - h²)/a.
Отсюда выразим гипотенузу Г:
Г = a/sin A = a/(√(a² - h²)/a) = a²/√(a² - h²).
В прямоугольном треугольнике медиана m к гипотенузе равна её половине.
ответ: m = a²/(2√(a² - h²)).