это ответ б
там все на 5 делят
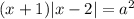
Первый аналитический)
1) Если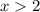 
, то 
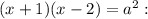
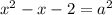
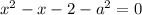
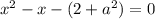
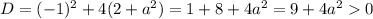
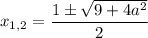
Проверим условие 
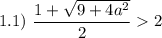
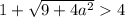
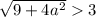
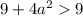
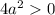
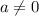
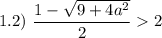
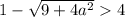
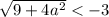
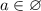
Таким образом, если 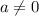, то имеем корень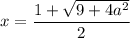 
2) Если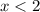 
, то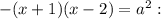 
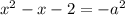
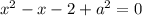
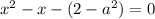
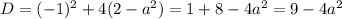
Найдем такие значения 
, при которых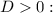 
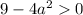
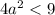
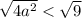
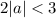
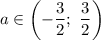
Тогда корни:
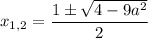
Проверим условие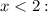 
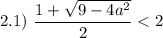
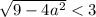
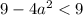
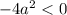
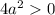
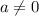
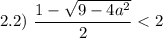
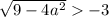
![a \in \left[-\dfrac{3}{2}; \ \dfrac{3}{2} \right]](/tpl/images/1359/4428/7966b.png)
С учетом 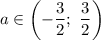имеем: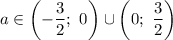 
Таким образом, при 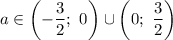имеем три корня.
Второй графический)
Рассмотрим две функции:
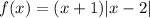
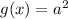— линейная функция, график — прямая, параллельная оси абсцисс
Изобразим на координатной плоскости функцию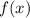 
1) Если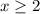 
, то 
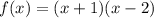— квадратичная функция, график — парабола, ветви параболы направлены вверх
2) Если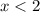 
, то 
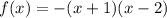— квадратичная функция, график — парабола, ветви параболы направлены вниз
Вершина параболы: 
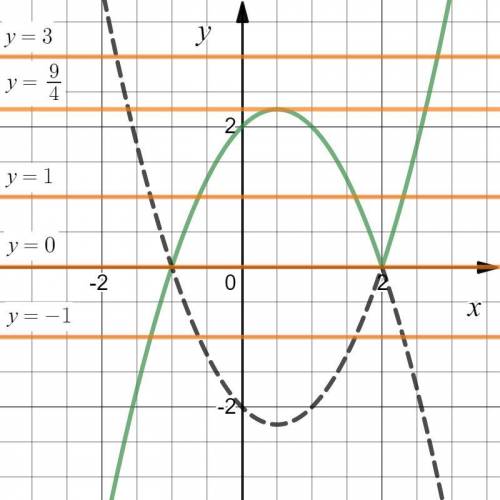
Изобразим данные функции на соответствующих участках (см. вложение).
Уравнение 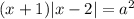будет иметь три корня, если будет три пересечения графика функции 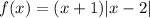c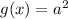
Так будет, ес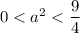ли 
или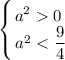 
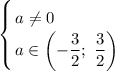
Решением системы будет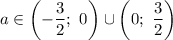
Таким образом, при 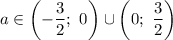имеем три корня.
ответ: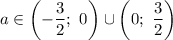
ответ - б
почему?
чем отличаются арифметическая и геометрическая прогрессии.
первая получается ходом прибавления или вычитания одного и того же числа
а вторая - умножением или делением.
первая последовательность является последовательностью чисел 1 и 2, не относящихся ни к арифм. не геом. погрессиям
в и г - арифметические т.к. образуются путем прибавления и вычитания одного и того же числа.
а б - путем деление на 5.