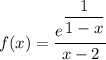1. Рассмотрим точку 11. Тут явно разрыв, так как функция не определена
2. Вычислим односторонние пределы
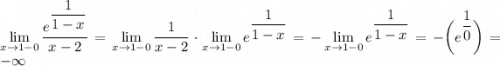
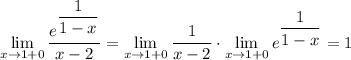
То есть функция сначала ушла в -∞ а затем резко появилась в 1
это разрыв второго рода
2. Рассмотрим точку 21. Тут опять разрыв, смотрим какой
2. Вычислим односторонние пределы
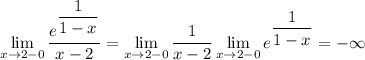
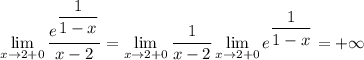
То есть функция сначала уходит в -∞ а потом выходит из +∞
В этой точке тоже разрыв второго рода
кор. абел.аволн.вгл. вр: аавв(кор, волн) х аавв(бел. гл.)g: ab ; aвf: аавв (кор. волн) рf1: аавв (кор, волн) х аавв (кор., волн)g: ав, ав, ав, ав ; ав, ав, ав, авf2: аавв (кор, волн)аавв (кор, волн)аавв(кор, волн)аавв(кор, волн)аавв(кор волн)аавв(кор. гл.)аавв(кор, волн)аавв(кор, гл)аавв(кор. волн)аавв(кор, волн)аавв (бел, волн)аавв (бел. волн)аавв( кор, волн)аавв(кор, гл)аавв(бел. волн)аавв(бел, гл)расщепление по фенотипу: 9: 3: 3: 14 группы животных, потому что, родители были дигетеорзиготы