Да, молния - это гигантская электрическая искра
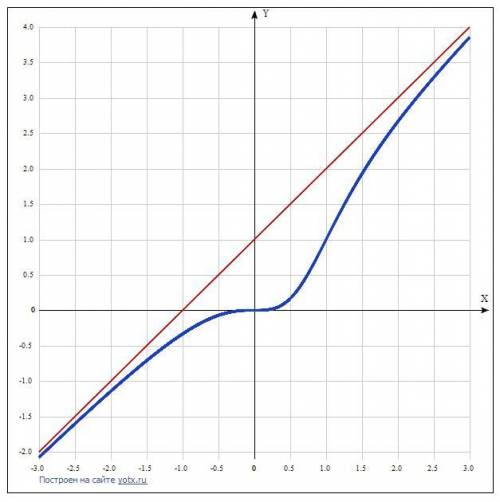
Дана функция y=x^3/(x^2-x+1).
План исследования:
1)Найти область определения ф-ции, интервалы непрерывности и точки разрыва ф-ции .
Исследуем знаменатель на возможность равенства нулю.
Выражение: x^2-x+1=0.
Ищем дискриминант: D=(-1)^2-4*1*1=1-4=-3;
Дискриминант меньше 0, уравнение не имеет корней.
Значит, функция не имеет ограничений. х ∈ Z.
2)Чётность и нечётность: f(-x) = -x^3/(x^2+x+1) ≠ f(x) ≠ -(f(x).
Функция общего вида.
3)Найти точки пересечения с осями координат.
- с осью Оу при х = 0, у = 0.
- с осью Ох при у = 0.При этом надо числитель приравнять нулю.
Получаем х = 0.
4)Определить интервалы возрастания и убывания, экстремумы ф-ции .
Производная функции равна: y' = (x²(x² - 2x + 3))/(x²- x + 1)².
Приравняем нулю числитель: x²(x² - 2x + 3) = 0.
Один корень получаем: х = 0.
Далее приравниваем нулю второй множитель. x² - 2x + 3 = 0.
Д = 4 - 4*1*3 = -8. Корней нет. Одна критическая точка х = 0.
Для определения характера этой точки определяем знаки производной левее и правее точки х = 0.
x = -1 0 1
y' = 0,667 0 2 .
Как видим, эта точка не является экстремумом функции.
На всей области определения функция возрастает (производная везде положительна).
5)Найти интервалы вогнутости и выпуклости, точки перегиба.
Вторая производная (её нахождение сложное и громоздкое) имеет нули в двух точках: х = 0 и х = 1. Это точки перегиба.
График вогнут на промежутке (0; 1).
График выпуклый на промежутках (-∞; 0) и (1; +∞).
6) Определить асимптоты.
Уравнение наклонной асимптоты имеет вид y=kx+b. Наклонную асимптоту можно найти, подсчитав предел данной функции, деленной на x при lim┬( x→±∞)〖(kx+b-f(x)).〗
Находим коэффициент k: k=lim(x→±∞)〖(f(x))/x.〗
k= lim(x→∞)〖x³/((x²-x+1)* x)=x²/(x²-x+1)=(x²/x² )/((x²/x²) - (x/x²) + (1/x²) =1/(1+0+0)=1.〗
Коэффициент b: b=〖lim(x→±∞) (〗〖f(x)-kx).〗
Аналогично коэффициенту к находим b = 1.
Уравнение наклонной асимптоты у = х + 1.
7)Построить график по точкам:
x y
-3.0 -2.08
-2.5 -1.6
-2.0 -1.14
-1.5 -0.71
-1.0 -0.33
-0.5 -0.07
0 0
0.5 0.17
1.0 1
1.5 1.93
2.0 2.67
2.5 3.29
3.0 3.86
Кладовщик выдал по первому ордеру две седьмых всей имевшейся на складе проволоки, а по второму ордеру-три четырнадцатых всей проволоки. Сколько килограммов проволоки было на складе, если по первому ордеру было выдано на 25 кг больше чем по второму?
1 орден -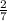 
2 орден -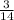 
на 25 кг меньше чем на 1 орден
было 1 (единица) - это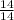 
составим уравнение
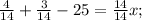
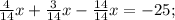
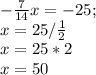
теперь найдем на первом и на втором
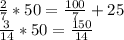
сколько они всего выдали за 2 ордена
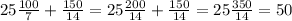
2 ордена это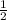 
всех. Значит дамножим на 2 и получим 100
Я думаю может быть д