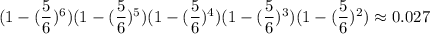Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда
Вероятность не угадать число на одном кубике равна (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна - это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна
Ябл, Гр, Ап. Всего 5 шт; Ябл. ? шт, но на 2>Гр. Гр ? шт; Ап. ? шт Решение. 1). Подбор: Фруктов мало, их три вида, а всего 5 шт., поэтому груш, возможно, 1. Тогда яблок 1+ 2 = 3 (шт), и апельсинов будет: 5 -1 -3 =1 (шт.) ответ: 3 груши, 1 апельсин, 3 яблока. 2). Уравнивание. 5 - 2 = 3 (шт.) количество фруктов, если убрать "лишние" яблоки. 3 : 3 = 1(шт.) количество каждого фрукта (и груш в том числе!) без "лишних" яблок. 1 + 2 = 3 (шт.) яблок на самом деле. ответ: 3 яблока, 1 груша, 1 апельсин в вазе. Проверка: 3 + 1 + 1 = 5; 5 = 5.
Других вариантов нет, так как : а) если груш 2, то яблок будет уже 2 + 2 = 4, а всего яблок и груш тогда 2 + 4 = 6, что противоречит условию, так как всего фруктов 5; б) если груш НЕТ, то яблок 0+2=2, а апельсинов 5-2=3, но по условию у нас три вида фруктов.
Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков
Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда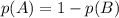
Вероятность не угадать число на одном кубике равна
(среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна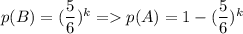 
- это и есть искомая вероятность в данной задаче.
Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна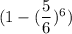
. При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 
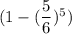. При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна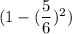 
Тогда искомая вероятность