Геометрический смысл определенного интеграла - площадь фигуры под графиком функции. Таким образом, задача сводится к вычислению определенного интеграла. Сначала следует определить пределы интегрирования. Для этого нужно найти пересечения кривой с осью x (y=0):
Надо брать эти числа и делить на самые маленькие без остатка. К примеру, число 875 делим на 5, получаем 175, делим еще на 5, получаем 35, делим еще на 5, получаем 7. Значит, 875 = 7*5*5*5 2376 делим на 2, получаем 1188, опять делим на 2, получаем 594, снова делим на 2, получаем 297, делим на 3, получаем 99, делим на 3, получаем 33, делим на 3, получаем 11. Значит, 2376=11*3*3*3*2*2*2 и так далее. При разложении простые правила: если число оканчивается на 0 или на 5, оно делится на 5, если сумма цифр в числе делится на 3, число делится на 3, если число оканчивается на четную цифру, оно делится на 2
Надо брать эти числа и делить на самые маленькие без остатка. К примеру, число 875 делим на 5, получаем 175, делим еще на 5, получаем 35, делим еще на 5, получаем 7. Значит, 875 = 7*5*5*5 2376 делим на 2, получаем 1188, опять делим на 2, получаем 594, снова делим на 2, получаем 297, делим на 3, получаем 99, делим на 3, получаем 33, делим на 3, получаем 11. Значит, 2376=11*3*3*3*2*2*2 и так далее. При разложении простые правила: если число оканчивается на 0 или на 5, оно делится на 5, если сумма цифр в числе делится на 3, число делится на 3, если число оканчивается на четную цифру, оно делится на 2
Геометрический смысл определенного интеграла - площадь фигуры под графиком функции. Таким образом, задача сводится к вычислению определенного интеграла. Сначала следует определить пределы интегрирования. Для этого нужно найти пересечения кривой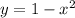 с осью x (y=0):
с осью x (y=0):
Получаем такой интеграл: