B ның қандай мәндер жиынында 3b-2өрнегінің мәндері [-3;3]аралығына тиісті болады

👇

Открыть все ответы

Ответ:

MHEBCEPOBHO

24.09.2020

Дана кривая 3x² - y - 2x - (14/3)=0.
Выразим относительно у:
у = 3x² - 2x - (14/3).
Находим координаты вершины параболы:
Хо = -в/2а = 2/(2*3) = 2/6 = 1/3.
Уо = 3*(1/9) - 2*(1/3) - (14/3) = (1/3) - (2/3) - (14/3) = -11/3.
Так как вершина ниже оси Ох, то парабола пересекает её в двух точках.
Приравниваем нулю:
3x² - 2x - (14/3) = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-2)^2-4*3*(-14//3)=4-4*3*(-(14//3))=4-12*(-(14//3))=4-(-12*(14//3))=4-(-56)=4+56=60;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√60-(-2))/(2*3)=(√60+2)/(2*3)=(√60+2)/6=√60/6+2/6=√60/6+(1//3) ≈ 1.624328;x_2=(-√60-(-2))/(2*3)=(-√60+2)/(2*3)=(-√60+2)/6=-√60/6+2/6=-√60/6+(1//3) ≈ -0.957661.

График и таблица дополнительных точек для его построения приведены в приложении.

Назвать и построить кривую 3x^2-y-2x-14/3=0

Назвать и построить кривую 3x^2-y-2x-14/3=0

4,5(70 оценок)

Ответ:

dimidom56

24.09.2020

Пошаговое объяснение:

Пропорция – это равенство, утверждающее, что два отношения равны. Пропорция всегда включает равные коэффициенты. Пропорция состоит из двух равных отношений.

$\displaystyle \frac{a}{b}=\frac{c}{d}$

Для того , чтоб составить пропорции из данных выражений , надо представить их в виде обыкновенной дроби . Равные дроби - равные отношения , соответственно это и будет пропорцией.

Представим отношение в виде обыкновенной или неправильной дроби и сократим :

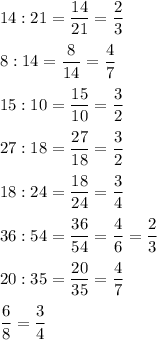
$\displaystyle 14:21=\frac{14}{21}=\frac{2}{3} \\ \\ 8:14=\frac{8}{14}=\frac{4}{7}\\ \\ 15:10=\frac{15}{10}=\frac{3}{2}\\ \\ 27:18=\frac{27}{18}=\frac{3}{2}\\ \\18:24=\frac{18}{24}=\frac{3}{4}\\ \\ 36:54=\frac{36}{54}=\frac{4}{6}=\frac{2}{3}\\ \\ 20:35=\frac{20}{35}=\frac{4}{7}\\ \\ \frac{6}{8}=\frac{3}{4}$

Выберем равные дроби :

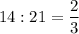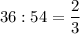
$\displaystyle 14:21=\frac{2}{3}$ и $\displaystyle 36:54=\frac{2}{3}$

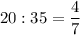
$\displaystyle 8:14=\frac{4}{7}$ и $\displaystyle 20:35=\frac{4}{7}$

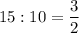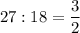
$\displaystyle 15:10=\frac{3}{2}$ и $\displaystyle 27:18=\frac{3}{2}$

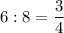
$\displaystyle 18:24=\frac{3}{4}$ и $\displaystyle 6:8=\frac{3}{4}$

Теперь можем составить пропорции и проверим правильность с основного правила пропорции : произведение крайних членов пропорции равно произведению средних членов пропорции.

1) 14 : 21 = 36 : 54

проверим

14 * 54 = 21 * 36

756 = 756

получили верное равенство , значит пропорция верная.

2) 8 : 14 = 20 : 35

8*35 = 14 * 20

280 = 280

3) 15 : 10 = 27 : 18

15 * 18 = 10 *27

270 = 270

4) 18 : 24 = 6 : 8